Viana, V. Archimedean solids in the fifteenth and sixteenth centuries. Archive for History of Exact Sciences 78, 631–715 (2024). https://doi.org/10.1007/s00407-024-00331-7

1 Introduction

In the fifteenth and sixteenth centuries, the enthusiasm from scholars, mathematicians, artists, and artisans for the solid bodies that we came to identify as polyhedra was so significant that the knowledge they developed on the subject marks the Renaissance and Mannerism periods as a milestone in the history of polyhedra.^{Footnote 1} Much of this interest derived from the humanist mathematicians who developed the scholarship on Archimedes, Ptolemy, and Euclid^{Footnote 2} but the publication of the Timaeus^{Footnote 3} and the Elements also played a significant role in this matter, especially Books XIV and XV, which were accepted in the Middle Ages as having been written by Euclid. Book XIV comprises the studies of Hypsicles of Alexandria (c.190–c.120 BCE) on the regular bodies. Book XV, according to Scriba and Schreiber (2015, p. 100), would have been written by an unknown Byzantine mathematician from the fifth or sixth centuries, and explains how to inscribe the Platonic Solids in each other.^{Footnote 4} The spurious books were included in the translation of the Elements into Latin by Campanus of Novara (1220–1296), first printed in 1482. The influence of this translation extended well into the sixteenth century as Luca Pacioli revised and republished it in 1509, even after Bartolomeo Zamberti (1473–1543), who translated the Elements from a Greek manuscript in 1505, had exposed Books XIV and XV as not having been authored by Euclid. Other translations of the Elements would follow but the translation into Latin by Federico Commandino published in 1572, according to Cromwell (1997, pp. 108–109), was so important it prevailed until the nineteenth century.

A few books published in the fifteenth and sixteenth centuries illustrating solid geometry concepts had a significant impact and their influence extended beyond their time and country of publication. The printing press, introduced in Europe in the mid-fifteenth century, was crucial to this evolution and developed steadily throughout the sixteenth century, enormously affecting society and culture. Hundreds of printing shops opened in major European cities, leading to a quicker and less expensive production of books and allowing printed publications to be accessible to everyone or, at least, to those who could buy and read them. With such a stimulating atmosphere, education and literacy grew within the middle classes and democratization of knowledge changed society for the better. Scholars and artists had an unprecedented opportunity to learn from books and libraries and share their knowledge by publishing their studies, while printing shops turned into new centres for intellectual exchange. The cities of Nuremberg, Venice and Antwerp became notable hubs in Europe because of their book production.^{Footnote 5}

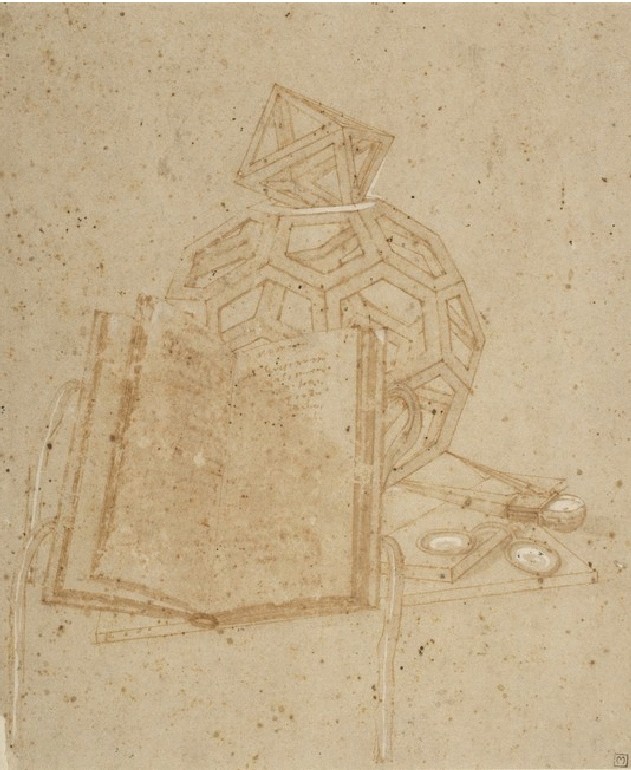
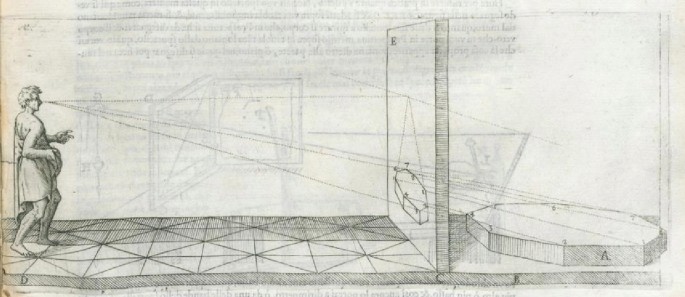
The development of perspective drawing was another cause for the fascination with solid bodies during the Renaissance and Mannerism, as they provided ideal subjects to practice the rules of perspective.^{Footnote 6} Drawing models of solid bodies became a regular practice for artists. Figure 1 shows an example of a truncated icosahedron and an octahedron drawn with a large portion of their faces hollow, much like those Leonardo da Vinci drew in vacuum mode for Divina Proportione, the book that Luca Pacioli published in 1509. Reciprocally, the drawing in Figure 2, from Le Due Regole della Prospettiva Pratica by Jacopo Barozzi da Vignola (1507–1573) and Egnazio Danti (1536–1586), uses an octagonal prism to explain the fundamentals of perspective drawing. The treatise by Vignola-Danti^{Footnote 7} (1583), published a few years after La Pratica della Perspettiva by Daniele Barbaro, was an important vehicle to disseminate the rules of perspective drawing among artists until the seventeenth century.

Further examples revealing an extraordinary mastery of perspective drawing in the depiction of polyhedral forms are the intarsias from the late fifteenth to the seventeenth centuries, and additional testimonies of the interest in solid geometry in the Italian Renaissance and Early Modern Germany.^{Footnote 8} Many intarsias depict exquisite polyhedral forms and a few testify a direct inspiration from Leonardo’s drawings, as Hart (1998) points out. An example is the intarsia on the left in Figure 3, whose forms above and below the cuboctahedron are almost exact copies of the “hexaedron elevatum vacuum” and the “dodecaedron abscisum elevatum vacuum” that Leonardo (1509, Plates XII and XXXIIII) drew for Divina Proportione. The truncated icosahedron in the intarsia on the right is an even more flagrant example since it copies a mistake from a manuscript version.^{Footnote 9} Such appropriations reveal that Divina Proportione was as much a cause as an effect on the overall fascination about polyhedra of its time, much of which derived from Leonardo’s impressive illustrations that, to this day, remain inspirational.

2 Consistent studies on the Archimedean solids during the 15^th and 16^th centuries

The Archimedean Solids are all the convex uniform polyhedra besides the Platonic Solids^{Footnote 10} and the infinite families of semiregular prisms and anti-prisms. There are thirteen Archimedean Solids, all of which are semiregular or vertex-transitive polyhedra, meaning that each of their vertices can be transformed into any other by a symmetry operation.^{Footnote 11} The cuboctahedron and the icosidodecahedron are quasiregular because they are also edge-transitive, as different faces intersect on every edge.^{Footnote 12} The names with which we identify the Archimedean Solids follow Wenninger (1975, pp. 20–32).

Pappus of Alexandria (c.290–c.350 CE) wrote the compendium of mathematics Synagoge around 340 CE. In Book V, Pappus credits the thirteen solid bodies to Archimedes (c.287–c.212 BCE) and describes the configuration and number of their faces. Pappus’ compendium would become widely known among European mathematicians after Federico Commandino translated it into Latin in 1588. The thirteen solid bodies would be coined as Archimedean Solids because Johannes Kepler (1571–1630) referred to them, in “XXVIII Propositio” of the Harmonices Mundi (1619, p. 19), in the following way:

As to the solids with an inferior degree of perfect proportion, there are thirteen species; from which the thirteen bodies of Archimedes derive.^{Footnote 13}

No evidence has been found supporting the possibility that the authors who explored these solid bodies before Kepler had any knowledge about Pappus’ compendium. In the opinion of Jones (1986, p. 50), the fact that Piero della Francesca described only six solid bodies suggests that he discovered them independently. Jones further notes that there is no direct evidence of any influence of the Synagoge on Piero or any other author who described the Archimedean Solids before Kepler.^{Footnote 14} The authors who rediscovered those that came to be known as Archimedean Solids did not know who had first described them or that they existed in a finite number – in fact, most authors tell us quite the opposite. Searching for these new forms derived from the Platonic Solids was a challenge in itself and a clear testimony to the inventiveness and geometrical knowledge of those who explored them.

We have been searching for polyhedral forms in historical books and treatises to understand how they were devised with the possibilities of their time. This essay brings forth our conclusions about the Archimedean Solids described in the fifteenth and sixteenth centuries,^{Footnote 15} and focuses on the manuscripts and publications whose studies revealed to be systematic and consistent: beginning with Trattato d’Abaco, which Piero della Francesca wrote between 1460 and 1480, and finishing with Problematum Geometricorum, which Simon Stevin published in 1583 and seems to have been the last study to include a systematic treatment of the Archimedean Solids before Kepler’s in 1619. Identifying with certainty who first described each of these solid bodies after Archimedes was a difficult task, given that none of the authors acknowledges previous sources nor (apart from one author) formally declares credit for their findings. Even Piero della Francesca, who may have been a precursor to all, was also influenced by others before him, so we can only take for granted that the influences that determined the discoveries and rediscoveries of solid bodies in the fifteenth and sixteenth centuries were complex and occasionally mutual.

Two of the first printed books that explain and illustrate solid geometry concepts had a seminal importance in their time and beyond: the first was the Divina Proportione that Luca Pacioli wrote between 1496 and 1498 and includes several drawings by Leonardo da Vinci, gathered at the end of the book. The second was Underweysung der Messung mit dem Zirckel und richtscheyt in Linien Eben un ganzen Corporen (hereon abbreviated to Underweysung der Messung). Written and illustrated by Albrecht Dürer, it was first published in 1525 and posthumously in 1538^{Footnote 16}. The following authors, who lived in the German States^{Footnote 17}, were strongly influenced by Pacioli/Leonardo and Dürer. Their books include impressive drawings of polyhedral forms, but were not necessarily intended to teach the rules of perspective drawing^{Footnote 18}: Geometria (1543) by Augustin Hirschvogel; Der Circles und Richtscheyts (1564) by Heinrich Lautensack (1522–1590); Perspectiva Literaria (1567) by Hans/Johannes Lencker (1523–1585); Perspectiva Corporum Regularium (1568) by Wentzel Jamnitzer; Geometria et Perspectiva (1567) and Geometria et Perspectiva Corporata et Regulata (1600) by Lorenz Stöer. Other authors were so impressed with the exquisite solid bodies in Jamnitzer’s book that they would describe similar forms on their own: Paul Pfinzing (1554–1599), in Extract der Geometriae vnnd Perspectiuae (1599) and Optica, das ist Gründtliche doch Kurtze Anzeigung Wie nothwendig die Löbliche Kunst der Geometriae seye inn der Perspectiv (1616); and Peter Halt (1575-after 1635) in Perspectiuische Reiss Kunst (1625) and Drey Wichtige newe Kunstst uck in underschidlichen (1626).

In Venice, Daniele Barbaro published the treatise La Pratica della Perspettiva (1568), whose Terza Parte is entirely dedicated to solid geometry. Rafael Bombelli began an interesting research on the semiregular bodies but no records exist beyond those in manuscript B 1569 of the Archiginnasio Library in Bologna, which Ettore Bortolotti (1929) edited in the twentieth century. Other remarkable works are La Pratica di Prospettiua del Caualiere Lorenzo Sirigatti (1596) by Lorenzo Sirigatti (1557–1578), as well as Livre de Perspective (1560) by Jehan Cousin (1490–1560) and Leçons de Perspective Positive (1576) by Androuet du Cerceau the Younger (1515/20–1585/86). The way in which all these artists and mathematicians graphically described polyhedral forms, either convex or concave, simple or compound, intensified the curiosity for polyhedra in their time and were determinant to subsequent research on polyhedra.

2.1 Piero della Francesca

Piero della Francesca (1415–1492) was a fundamental influence for many authors of his time and beyond because of his knowledge of perspective drawing, explicit in his paintings and the treatise De Prospectiva Pingendi. Piero translated and cited a manuscript authored by Archimedes,^{Footnote 19} and wrote two manuscripts on traditional mathematics: Trattato d’Abaco and Libellus de Quinque Corporibus Regularibus (heron abbreviated to Libellus). No certainties exist as to when he began the latter but it would have been finished, according to Andersen (2009, p. 35), between 1482 and his death in 1492. Piero was not only an artist, but a mathematician (according to Ciocci (2017, p. 32), one of the most important Italian mathematicians of the second half of the fifteenth century), yet his approach to mathematics was mostly based on the study of proportions.^{Footnote 20} The following is an example of the relationships Piero^{Footnote 21} establishes between the elements of a regular tetrahedron, which can be solved with the “Rule of Three”^{Footnote 22}:

A body of four equilateral triangular bases whose axis is 4.

We want to know the diameter of the sphere that contains it.

Knowing that in every equilateral body of four triangular faces, the proportion between the axis and its edge is the same as the proportion between the edge and the diameter of the sphere that contains it; the axis of the body of four faces is to the diameter of the sphere that contains it as 2 is to 3.^{Footnote 23}

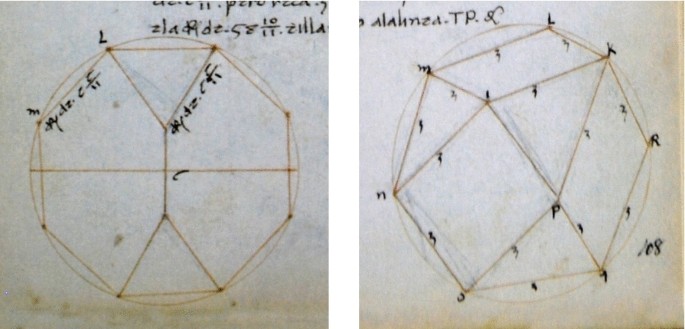
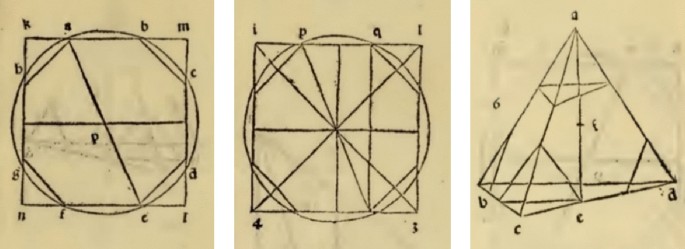
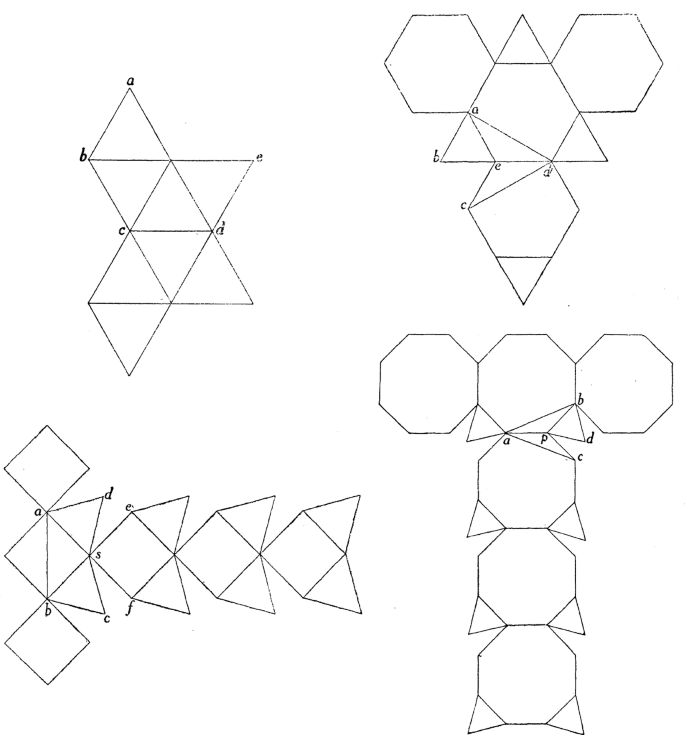
The two treatises written by Piero discuss the regular bodies described in the Elements and others derived from them. Given that a clear comprehension of the distances between elements in all the drawings was essential, Piero chose the “paralleli modo” to illustrate his studies on solid geometry. The parallel mode provided a simple representational method with which the illusion of depth for small objects is easily created without a perspectival construction.^{Footnote 24} The objects are drawn as if they were being observed from a short distance and any parallelism between the edges is preserved. In specific situations, certain faces are drawn in true form, allowing Piero to illustrate the relationships between measurements better. Occasionally, the parallelism is not accurate but Piero adds annotations to clarify measurements and other details. Figure 4 shows an example, in which the notations clarify that all the edges of the cuboctahedron have the same length. Scolari (2015, p. 217) explains that these numerical indications placed near the edges are meant to “correct the viewer’s perception of the measurements.”

Piero may have taken inspiration from the medieval version of the Elements to describe six Archimedean Solids, as Field (1997, p. 246) suggests, by referring to Books XIV and XV as “the likeliest source for Piero della Francesca’s rediscovery of some of the Archimedean solids”. Piero illustrates the truncated tetrahedron and the cuboctahedron in Trattato d’Abaco (Figure 4), and again in the Libellus, together with the truncated icosahedron, truncated dodecahedron and the truncated cube (Figure 5). Contrary to the remaining solid bodies, Piero drew the truncated tetrahedron as if it were transparent, most likely, because this was the simplest way to illustrate how to obtain it from the tetrahedron. Piero also describes the truncated octahedron in the Libellus as one of the irregular bodies circumscribed by the sphere, yet no drawings are shown. This is the fourth case in the Tertius Tractatus, and is described as the body with 14 bases, 6 of them squares and 8 hexagonal or, in the translation by Pacioli (1509, folio 21v, Tertius Tractatus), “il corpo de 14 base cioe 6 quadrate e 8 exagone”.

Piero drew a few cases in what we may interpret as orthographic projections: the truncated tetrahedron in Figure 4 and two of what may be construed as different plan-views of a truncated cube in Figure 5. A certain level of imprecision is understandable and even if Piero had built a three-dimensional model of these solid bodies, it could not have been easy to understand that, in the first case, the orthogonal projection of eight vertices belongs to the circle that Piero drew, but the circle itself is not the orthogonal projection of a great circle of the sphere that encloses the truncated tetrahedron. In the second, the orthogonal projection of eight vertices belongs to the circle in the rightmost drawing, yet the circle itself is not the orthogonal projection of the circumsphere of the truncated cube. Piero’s descriptions of solid bodies are unquestionably remarkable not only for their inventiveness, but because they introduce a conscious search for other than Euclid’s regular bodies, paving the way for all subsequent rediscoveries of the Archimedean solids, compounds, and other polyhedral forms.

2.2 Luca Pacioli and Leonardo da Vinci

In 1550, Giorgio Vasari tells us that Luca Pacioli (1447–1517) had copied the manuscripts of Piero della Francesca and published them as if they were his own. Many authors have discussed this subject^{Footnote 25} ever since, and if it were not for Pacioli’s plagiarism, the work that Piero developed on geometry and his important legacy as a mathematician would probably not be known today. In the opinion of Ciocci (2017, p. 104) Pacioli did not limit himself to usurping the works of others and asserts that it would be “historically reductive to maintain that everything Pacioli wrote on the subject of polyhedra was pillaged from the manuscripts of Piero”.

Pacioli brought some contributions to the treatment of the regular and irregular bodies proposed by Piero and imprinted his own perspective on the narrative. The names he gave to the solid bodies derived from the Platonic Solids are one example. Pacioli commissioned the illustrations of Pars Prima in Divina Proportione to Leonardo da Vinci (1452–1519), a wise decision that proved to be a fitting complement to what might have been a less interesting book. The drawings by Leonardo decisively emphasized the interest in polyhedral forms in the sixteenth century and contributed to the importance given to polyhedra as a mathematical subject in its own right. Although Luca Pacioli was not an artist but a mathematician, he praised the knowledge of perspective drawing and advocated for considering it a mathematical topic, according to Andersen (2009, p. 80), although no records exist of any perspective construction having been drawn or understood by him.

Replicating the deductions of Piero, Pacioli devised solid bodies from the Platonic, truncating their vertices after dividing the edges into two or three equal parts. Assuming that similar and sequential truncations of regular and irregular bodies would produce an infinite number of solid bodies, Pacioli (1509, folio 16v, Pars Prima) declares that he will not lose time in discussing them extensively, given that the forms in which they multiply, by continuous and successive cutting of their solid angles, tend to infinity.^{Footnote 26} Pacioli also conceived solid bodies through augmentation, joining regular-faced pyramids to the faces of other bodies, obtaining what we came to recognize as concave deltahedra. In his description of the augmented tetrahedron or “tetraedron elevatum”, Pacioli (1509, folio 14v, Pars Prima) says that the pyramid concealed within the four pyramidal surfaces is the interior pyramid that the eye cannot see, only the intellect: “che lochio non po veder ma solo l’intellecto la prende”. The “octaedron elevatum” is the stella octangula that Kepler would later describe. It is also the regular compound of two tetrahedra and the only stellation of the regular octahedron, precisely the one which, according to Pacioli, we can only imagine.

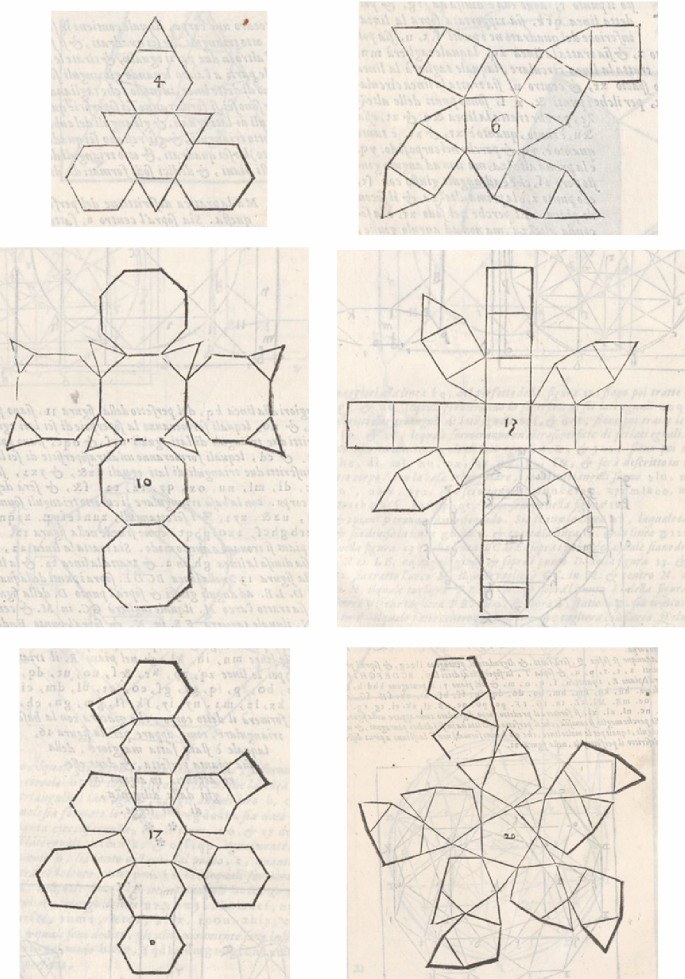
Two of the books that Pacioli wrote, Summa de Arithmetica, Geometria, Proportione et Proportionalita (1494) and Divina Proportione (1509), describe Archimedean Solids. Those in Summa, which are shown in Figure 6, and those in the margins of Divina Proportione, shown in Figure 7, were not drawn by Pacioli, but the printer to whom he would have handed a copy of Piero’s manuscript.^{Footnote 27} In comparison to the drawings by Leonardo in the last part of Divina Proportione, these drawings are very different, even uninteresting, we might say. On the other hand, the images of the solid bodies in solidum and vacuum display modes, shown in Figure 8, were drawn by Leonardo from physical models crafted in wood or cardboard that Pacioli owned. Pacioli (1509, folio 22, Pars Prima) refers to these in Divina Proportione.^{Footnote 28}

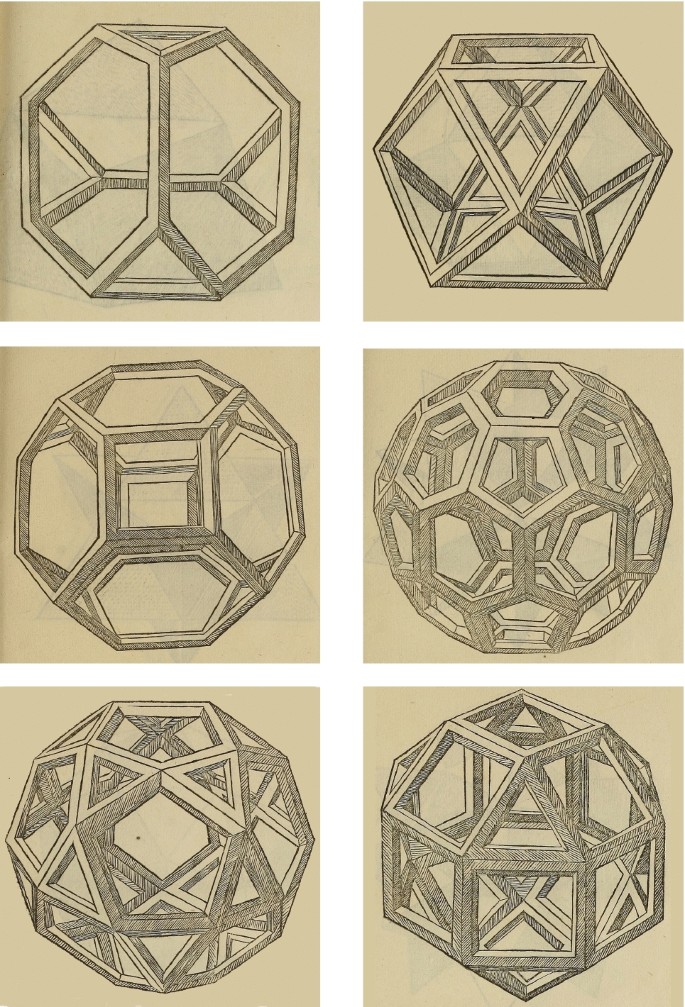
The Divina Proportione includes the first known graphic descriptions of the icosidodecahedron and the rhombicuboctahedron. In Pars Prima, the truncated tetrahedron is described as Chapter XLIV and illustrated by Leonardo (Figure 8) at the end of the book. The drawing of the truncated tetrahedron (Figure 7) in the Tertius Tractatus, however, was not done by Leonardo. Its depiction is substantially different from the one in Summa (Figure 6) and, for the known reasons, much closer to Piero’s drawing in the Libellus (Figure 5). Before introducing the truncated cube in the Tertius Tractatus, Pacioli (1509, folio 22, Tertius Tractatus) warns the reader that it was not possible to include figures for all the cases in the margins of the book since some were difficult to draw. It would have been necessary someone versed in perspective drawing for this purpose, he adds, as Leonardo da Vinci had been for Pars Prima. For this reason, Pacioli says that some solid bodies are discussed but no drawings will be shown in the margins of the book. However, since these tend to infinity, Pacioli adds, it will be enough for the readers to observe the drawings that Leonardo did and picture the rest for themselves.^{Footnote 29}

In Pars Prima, the sequence of irregular bodies contained within a sphere is not the same as in the Tertius Tractatus. Piero had begun with a Campanus sphere before addressing the truncated icosahedron, the truncated dodecahedron, the truncated octahedron, the truncated cube, and the truncated tetrahedron. We interpret this sequence as Piero’s choice of approaching the complex cases before the simplest: after the 72-faced, the body with 32 faces (pentagonal and hexagonal), followed by another, also with 32 faces (triangular and decagonal); the following with fourteen (triangular and octagonal); and the last with eight faces (triangular and hexagonal). With the exception of the truncated octahedron, Piero illustrated all of these. On the other hand, the sequence of solid bodies in Pars Prima reveals that Pacioli chose to explain the truncation of each of the convex regular. Omitting the augmented forms, Pacioli presents: after the tetrahedron, the truncated tetrahedron; after the cube, the cuboctahedron; after the octahedron, the truncated octahedron; after the icosahedron, the truncated icosahedron; and after the dodecahedron, the icosidodecahedron. All of these are directly obtained by truncation of the previous, whose edges are divided either into two equal parts (cuboctahedron and icosidodecahedron) or three equal parts (truncated tetrahedron, truncated octahedron and truncated icosahedron).

In his adaptation of the Libellus, Pacioli treats the truncated dodecahedron as the third case of the Tertius Tractatus, between the truncated icosahedron and the truncated cube. It had been illustrated by Piero and even mentioned by Pacioli in our previous footnote, yet there are no drawings of the truncated dodecahedron in Divina Proportione. Perhaps the person who was assisting Pacioli found it difficult to copy from Piero’s manuscript or maybe Pacioli decided that the body of the decagon was not as important as the other bodies. It seems, however, that Leonardo found it interesting because he drew it in folio 735v (Figure 9) of the Codex Atlanticus. The Codex Atlanticus compiles the numerous drawings and personal notes that Leonardo worked on between 1478 and 1519 and are preserved at the Veneranda Biblioteca Ambrosiana in Milan. Leonardo would have sketched folio 735 around 1495^{Footnote 30} precisely while he was preparing his drawings for Divina Proportione, which he concluded by the end of 1497, according to Huylebrouck (2015, p. 463). Leonardo may have taken inspiration for the truncated dodecahedron from Piero’s manuscript or maybe he devised it on his own, as suggested by Huylebrouck et al. (2020, p. 63).

Based on the notes that Leonardo wrote, Huylebrouck et al. (2020, pp. 62–64) interpret the drawing on the upper left in Figure 9 as an unfinished sketch of a truncated dodecahedron augmented with triangular pyramids and pentagonal cupolas. A pentagonal cupola has two parallel faces, pentagonal and decagonal, with triangular and quadrangular faces between them. Assuming that Leonardo intended all the faces to be regular, Huylebrouck et al. conclude that he devised two polyhedra that Norman Johnson (1966, pp. 185, 195) would describe centuries later: the pentagonal cupola and the augmented truncated dodecahedron (respectively, Johnson Solids J5 and J68). Huylebrouck at al. (2020, p. 64) further suggest that Leonardo could have obtained Johnson Solids J69, J70 or J71 if he had added two or three cupolas to specific faces. Field (1997, p. 263) notes that, in the sketch that resembles a rhombicosidodecahedron, Leonardo would have tried to obtain a solid body analogous to the rhombicuboctahedron. However, the “solid shown in his drawing is not possible in mathematical terms (unless some faces are not regular)”. Huylebrouck et al. (2020, pp. 62–63) assert that, as Leonardo explains in a side-note and although the sketch does not clearly show it, the darker triangles stand for pyramids adjoined to the triangular faces.

The sketch might not have been developed because it was only a study, but it may be interpreted as a partial representation of a concave polyhedron which, completed, would be composed of twelve pentagonal cupolas and twenty triangular pyramids, as interpreted in Figure 10. In this interpretation, all the faces, apart from the rectangular, are regular. With cupolas adjoined in this orientation, adjacent squared faces become rectangular while the triangular faces surrounded by the rectangles are coplanar. To circumvent this coplanarity, Leonardo adds pyramids between each triad of triangles, where the lesser faces of the truncated dodecahedron were. The sketch drawn by Leonardo cannot be taken as an attempt for a rhombicosidodecahedron because the resulting polyhedron, without the pyramids, has 30 rectangular and 120 triangular faces. However, sketching it from the implied truncated dodecahedron is strikingly inventive for Leonardo’s time. Decades later, Daniele Barbaro would describe a concave polyhedron with six pentagonal cupolas in a partial planar net^{Footnote 31} but the point of departure, in his case, was the rhombitruncated icosidodecahedron.

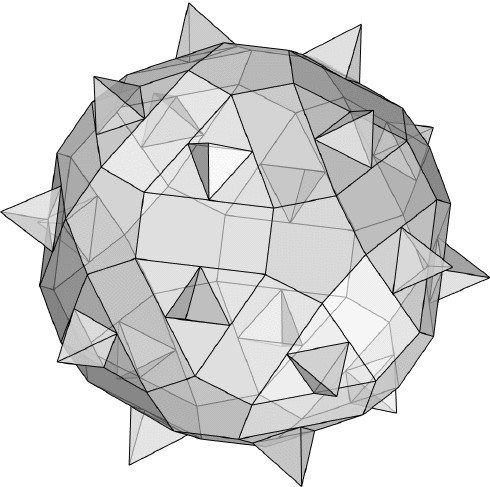
The central sketch in the bottom row in Figure 9 is a non-uniform version of a rhombitruncated icosidodecahedron with rectangular faces instead of squared. Huylebrouck et al. (2020, p. 66) discuss the possibility that it might have been meant as an augmented version of the rhombitruncated icosidodecahedron with square pyramids. Our analysis of the sketch leads us to believe that Leonardo arrived at the convex form by dividing the edges of an icosidodecahedron into three equal parts. If Leonardo had developed this study or built a model or its planar net, he would have concluded that it was possible to obtain a similar polyhedron with squares instead of rectangular faces. Although these and numerous sketches in the Codex Atlanticus are unfinished, they are remarkable in reaffirming Leonardo’s creativity and drawing mastery that vastly surpassed Pacioli’s guidance and are vivid testimonies of how Leonardo excelled in his “ability to imagine forms in space”, to use the words of Field (1997, p. 263).

2.3 Albrecht Dürer

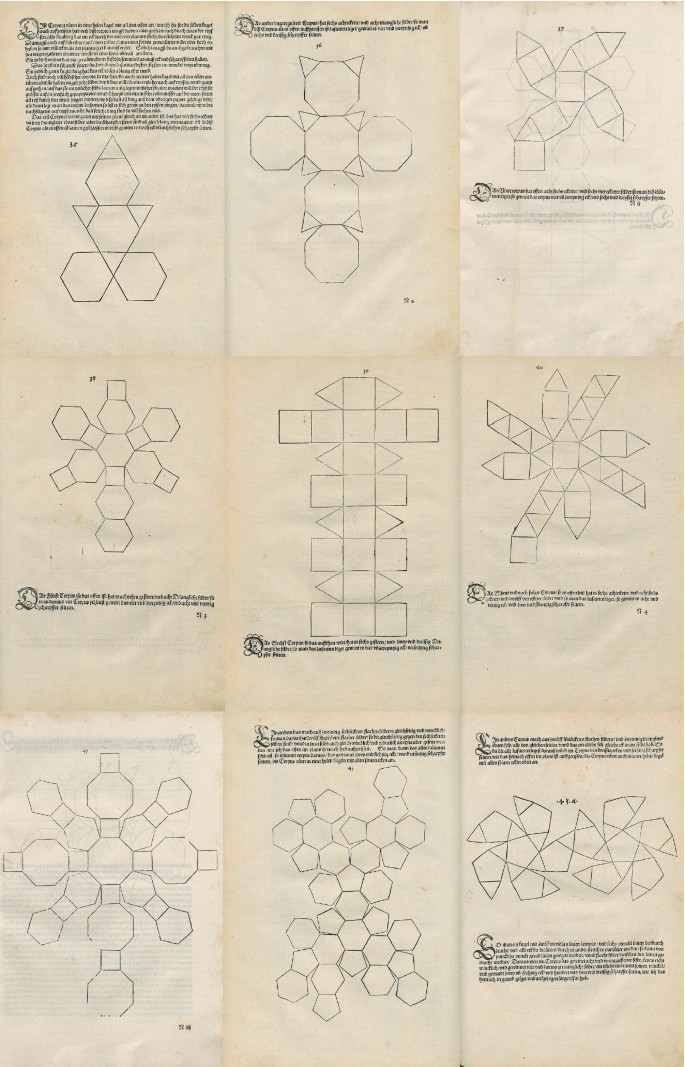
Albrecht Dürer (1471–1528) published the seminal treatise Underweysung der Messung in 1525. Written in German, it gained widespread recognition across various European regions after its translation into Latin by Joachim Camerarius (1500–1574) that was published in 1532.^{Footnote 32} A posthumous version of the first edition was published in 1538 by Hieronymus Andreae (c.1504–1556), the printer with which Dürer regularly worked and collaborated. According to Andrews (2016a, p. 409), Dürer worked on the revision of his treatise from 1525 until his death in 1528, and all the additions and annotations he did to his copy of the treatise “were carried over and faithfully reproduced” by Hieronymus Andreae.

In the 1525 edition, Dürer describes fourteen solid bodies. Each solid body is shown with a planar net but only the ones that Dürer refers to as those that Euclid names corpora regularia^{Footnote 33} are complemented with illustrations in plan and elevation. After describing the sphere, Dürer briefly introduces the ungeregulirten corporen, and when he describes them individually, he does not explain how each is obtained from which body; he only mentions the faces’ configuration and similar details. For those with regular faces, Dürer includes the number of vertices and edges; to those with other than regular faces, he gives details about the edges’ length. In his personal copy, Dürer added planar nets of two more irregular bodies: the truncated icosahedron and the icosidodecahedron, which are shown in Figure 11. Hieronymus Andreae would include these two extra bodies in the 1538 edition of Underweysung der Messung (1538), which includes a total of sixteen solid bodies. All their vertices, according to Dürer, touch a hollow sphere: the first five are the regular bodies; nine are Archimedean Solids (Figure 12), and two are non-uniform. Inspiration for the cuboctahedron, the truncated tetrahedron, the truncated cube, the truncated octahedron and the rhombicuboctahedron may have derived from Piero and Pacioli/Leonardo. However, after Archimedes, Dürer was the first to describe the snub cube and the rhombitruncated cuboctahedron.

Kemp (1992, p. 55) tells us that Dürer was introduced to visual geometry by a mathematician or a mathematically-minded artist in the orbit of Piero whom Dürer met in Bologna. In the opinion of Kemp, this person might have been Pacioli himself. In his second travel to Italy in 1505–07, Dürer could have met Luca Pacioli who, by then, had already concluded Divina Proportione and was working on his edition of the Elements. If Pacioli ever developed any friendship with Dürer, as Kemp suggests, he might have shared some thoughts about his upcoming book.^{Footnote 34} Indeed, Underweysung der Messung has many similarities with Divina Proportione but Dürer could have also known the book from Wilibald Pirckheimer (1470–1530), whose library he had access to, or from their occasional travels together.

If Dürer knew Divina Proportione when he was preparing his treatise (a task which, according to Kemp (1992, p. 55), he had begun around 1508), it is strange that the two solid bodies in Figure 11 were only added after 1525. Would this mean that Dürer browsed Divina Proportione in more detail only after his treatise was sent for printing? In any case, what seems clear to us is that Dürer consciously refrained from copying the conclusions of Pacioli/Leonardo, otherwise, he would have included planar nets for the icosidodecahedron and the truncated icosahedron in 1525. Peiffer (2000, p. 298) notes that Dürer owned a copy of Pacioli’s Summa but, as we have seen, these solid bodies are not included in this book. The fact that the truncated dodecahedron (which was graphically described by Piero but not by Pacioli) was not included in the 1525 or 1538 versions of the treatise implies that Dürer was also not adapting Piero’s findings, if he somehow had access to them.

Dürer bought Zamberti’s version of the Elements in 1507 and, in 1523, a set of books from the library of Regiomontanus–Walther, which included a copy of the Elements by Campanus of Novara, with comments from Johann Müller Regiomontanus (1436–1476)^{Footnote 35}. Much of Piero’s inspiration for the Archimedean Solids, we recall, came from Books XIV and XV of the medieval version of the Elements. This timeline leads us to believe that Dürer would only have had time to draw his conclusions from the analysis of Campanus’ version of the Elements sometime between 1525 and 1528, precisely while he was reviewing his own treatise. It is also interesting to note that most of the changes and additions Dürer introduced in his revision were, according to Andrews (2016a, p. 416), precisely in Book IV. From the handwritten changes in the first edition and the fact that Dürer devised two polyhedral forms that no one else in his time described, we can deduce that Dürer was not merely copying from Piero, Pacioli or Leonardo; he was studying polyhedral forms independently and, presumably, using Campanus’ Elements as a primary source for his research.

2.4 Augustin Hirschvogel

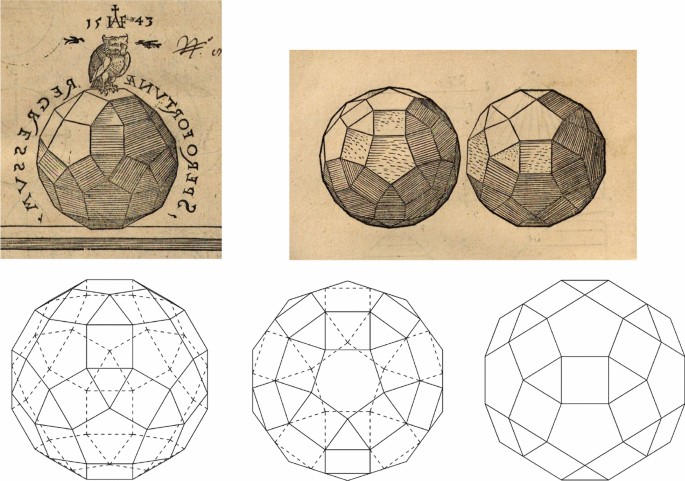
Augustin Hirschvogel (1503–1553) was a highly productive artist who excelled in etching, stained glass painting, and cartography. He was born in Nuremberg and traveled abroad in 1536 for work, returning to Nuremberg in 1543. In 1544, he relocated to Vienna, where he served as the city’s cartographer until his passing in 1553. Convinced of the importance of knowing geometry in his line of work,^{Footnote 36} Hirschvogel authored the book Geometria^{Footnote 37}, which was published in 1543. The cover (Plate AI in Figure 13) features the motto “Spero Fortunae Regressum” that encircles a rhombicosidodecahedron and was printed in a reflected version. According to Peters (2003), this sentence appears in two self-portraits dating from 1548 and denotes that Hirschvogel hoped to succeed in the imperial capital. Its meaning, I hope the return of fortune, tells us that Hirschvogel hoped for a better future as his life was not easy. The cover includes the delightful statement:

The book Geometria is my name

All free art first from me came

I bring architecture and perspective together^{Footnote 38}

Hirschvogel (1543) describes the seven Archimedean Solids shown in Figure 13 and Figure 14,^{Footnote 39} using the term “Geometria” to label his drawings of solid bodies. Six are illustrated with a planar net and plan views with shadows. The nets include auxiliary construction lines, while other sketches explain how to draw the plan views correctly. Five planar nets are equal to the ones Dürer included in the first edition of Underweysung der Messung. All are shown in the same position, except for the truncated cube, which is rotated

clockwise. However, the sequence in which the solid bodies are shown is not the same as Dürer because the icosidodecahedron comes between the truncated tetrahedron and the truncated cube. In the posthumous edition of Underweysung der Messung, the icosidodecahedron is the last of the additional bodies. Contrary to Dürer, Hirschvogel does not include the truncated icosahedron, the snub cube nor the rhombitruncated cuboctahedron. The net Hirschvogel conceived for the icosidodecahedron is very different from the one drawn by Dürer. It is also very distinctive given the interesting advantage he takes of its fivefold symmetry, which hints at the possibility that Hirschvogel studied it independently.

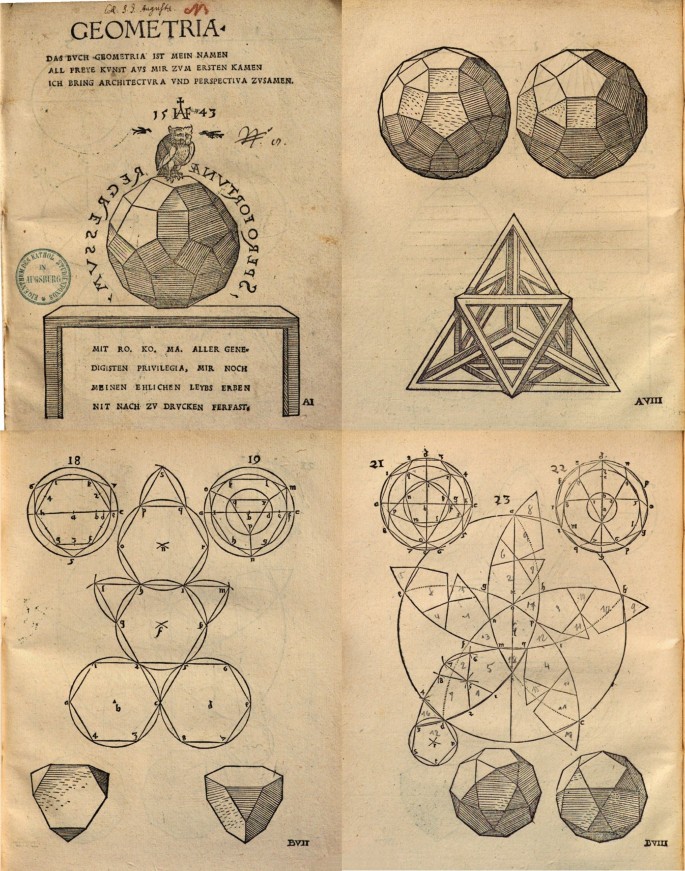
According to Friedman (2019, p. 69) and our own research, Hirschvogel was the first to describe the rhombicosidodecahedron after Archimedes. He illustrates it on the cover of his book (resting on what seems to be an engraved stone block) before introducing other drawings on solid geometry but he does not provide any auxiliary construction or net for the rhombicosidodecahedron, unlike other cases (the dodecahedron, described a few pages before, was also not described with a planar net). The three drawings in Figure 15 are essentially accurate and very close to orthographic projections: the first with two triangular faces in true form, while the second and third have two pentagonal and two squared faces in true form, respectively. The rightmost drawing in Plate A.VIII, however, contains a few errors: a trapezoid and a triangle are positioned on each side where a triangle and a parallelogram should be, respectively. In spite of these flaws, Hirschvogel drew the rhombicosidodecahedron in parallel perspective from different viewpoints with such accurate descriptions that it seems as if he was holding the object in his own hand. This leads us to suspect that he had a physical model crafted from a regular-faced planar net. The reason he did not include a complete description of the rhombicosidodecahedron with that planar net, as he had done to the remaining solid bodies, is unknown to us. Perhaps Geometria was the introduction to a more complex project which Hirschvogel could not develop where the rhombicosidodecahedron would be described in more detail.

Hirschvogel’s drawings of solid bodies are more detailed than those of his predecessors. In comparison, Wentzel Jamnitzer’s drawings, which would be published in 1568 in Perspectiva Corporum Regularium, are more visually appealing (see Figure 24). However, it should be noted that the purpose of Geometria was different from that of Perspectiva Corporum Regularium, and that the pages of the latter were printed from etched copper plates rather than engraved woodblocks. All the auxiliary lines in the solid bodies that Hirschvogel drew were printed with the same type and line weight as the edges, which makes some drawings difficult to understand at first sight. Printing different line types in a single woodblock may have been a technical predicament at the time, since the same happens in other books. In La Pratica della Perspettiva, for instance, which was printed in 1568, Barbaro (1568, pp. 60, 65) includes only two solid bodies with different line types: a cuboctahedron and a rhombicuboctahedron whose edges are printed in dotted line to illustrate their relation with a bounding cube, itself printed in continuous line. Interestingly, from the books printed in the German States on the subject, Perspectiuische Reiss Kunst by Peter Halt (1625), which would be published in 1625, seems to have been, if not the first, one of the firsts in which the hidden edges of solid bodies are drawn with dashed lines.

We have found very few drawings of the rhombicosidodecahedron after those drawn by Hirschvogel. Wentzel Jamnitzer drew the rhombicosidodecahedron which can be seen in Figure 24 in Perspectiva Corporum Regularium. Daniele Barbaro (1568, p. 96) included three drawings of the rhombicosidodecahedron in La Pratica della Perspettiva (one of which is shown in Figure 26). Despite minor inaccuracies, the drawings we found of the rhombicosidodecahedron between 1543 and 1568 are remarkably precise, given the complexity of this polyhedron. Another rhombicosidodecahedron still is in an etching authored by Hanns Sebald Lautensack (1520–1564/66) dating from 1553 and portraying the humanist Oswald von Eck (1539–1573) with a model of a rhombicosidodecahedron behind him (Figure 16). The Dictionary of Painters and Engravers, Biographical and Critical, by Michael Bryan (1886, pp. 26–27), mentions Hanns Sebald Lautensack and his brother, Heinrich Lautensack (1522–1568): the former as a skilled etcher^{Footnote 40}; the latter as a goldsmith and author of a treatise on perspective, Der Circles und Richtscheyts (1564). The fact that Hanns included a rhombicosidodecahedron in this etching may have been a contribution from his brother, who probably knew the book Hirschvogel wrote. Given its resemblance to the book cover in Figure 13, it might have been a direct copy from Hirschvogel’s Geometria since we have not yet found any description of the rhombicosidodecahedron by the Lautensacks before 1553.

2.5 An Anonymous Author

In New Light on the rediscovery of the Archimedean Solids during the Renaissance, Schreiber, Fischer and Sternath (2008) unveil the 40 printing woodblocks with planar nets of convex uniform polyhedra, found in the Albertina Museum in Vienna. Andrews (2016b, p. 247) shows a photograph of woodblock HO2006/693, with a planar net of the dodecahedron with an inscribed truncated icosahedron. Three woodblocks bear the signature of Hieronymus Andreae, the woodcutter responsible for both editions of Underweysung der Messung. Those unsigned may have been crafted by his workers, as suggested by Schreiber et al. (2008, p. 459), or left unfinished by Andreae himself. None of the woodblocks seems to have been used for other than test prints.^{Footnote 41} The Appendix of the Yearbook of the Art History Collections of the Highest Imperial House,^{Footnote 42} which Arpad Weixlgärtner (1910, p. 380) compiled in 1910, mentions a set of wooden blocks with geometric figures dated no later than the last quarter of the XVI century.^{Footnote 43} Whoever devised the planar nets in these woodblocks would have developed activities in Nuremberg or in close connection with the printing workshop of Hieronymus Andreae. In the following, we will refer to this person as the Anonymous Author.

According to Schreiber et al. (2008, pp. 459, 466), the Anonymous Author was “a remarkable forerunner” of Kepler who could not have been Dürer because the nets differ from those in his treatise, and because they include solid bodies that Dürer did not describe. Andrews (2016b, p. 36) adds that, unlike any of Dürer’s nets, some have “ornamental polygonal shapes composed of concentric lines covering portions of the nets’ faces”. Schreiber et al. believe the woodblocks were crafted between 1538 (the year in which the posthumous edition of Underweysung der Messung was published) and 1556, when Hieronymus Andreae died, and add that the person who conceived these planar nets had no knowledge of Pappus’ Synagoge because its translation into Latin would only be published in 1588. No early version of this translation would have been known in Europe before late 1560 since this was the year Commandino concluded his first draft.^{Footnote 44} Schreiber et al. further suggest that Johann Tscherte (1480–1552), a mathematician and friend of Dürer, may have been the Anonymous Author. Karl Weiß  (1894) tells us that Johann Tscherte was a master builder and an expert in fortification technology who moved to Vienna in 1510. In 1522, he stayed in Nuremberg during the Reichstag because of his sound knowledge of military buildings. In 1528, he was appointed bridge master in Vienna and later master builder, having collaborated on the defence of the city against the Turks. Tscherte was a friend of Willibald Pirckheimer and Albrecht Dürer, who authored his coat of arms in 1522.

Other than the suggestion of Schreiber et al. (2008, p. 467) about the identity of the Anonymous Author, we found no relevant connections between the activities of Tscherte and the depth of geometrical knowledge necessary to conceive the nets in these woodblocks, most of which are astounding, considering the knowledge and technical possibilities of their time. A woodblock we will not discuss in this study shows the nets of a triangular prism, a pentagonal prism, and a hexagonal anti-prism^{Footnote 45} which, in itself, is interesting not only for including an anti-prism but because whoever carved it placed the three together, as if the solid bodies differed from the remaining. In fact, they do, since they are examples of convex uniform polyhedra other than the Platonic and Archimedean Solids. As Coxeter (1973, 14) notes, Kepler is considered the first to have recognized the anti-prisms but these woodblocks were carved years before Kepler was born.

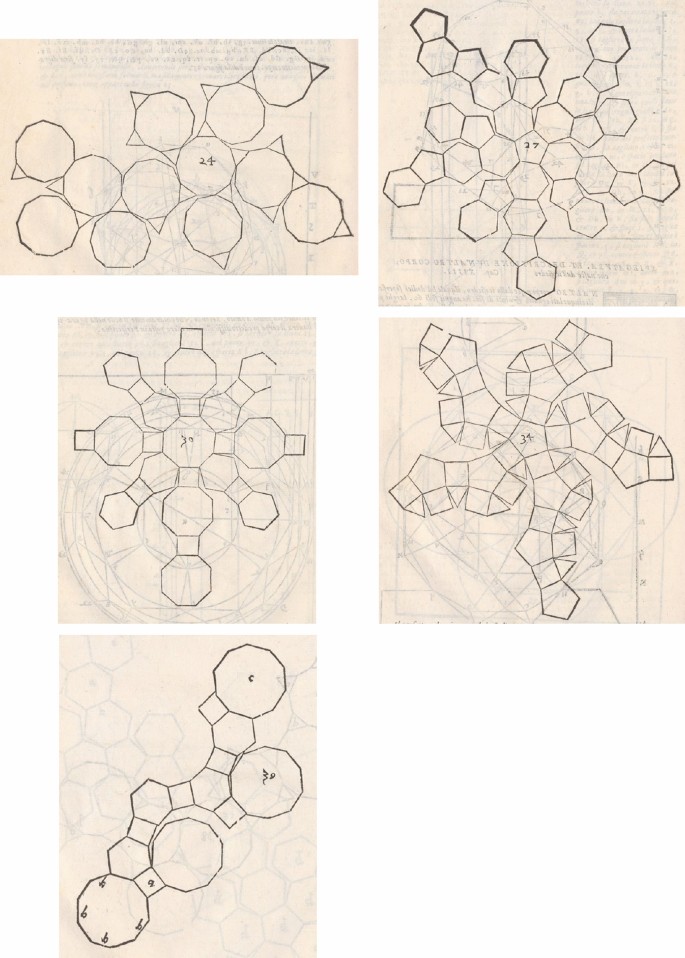
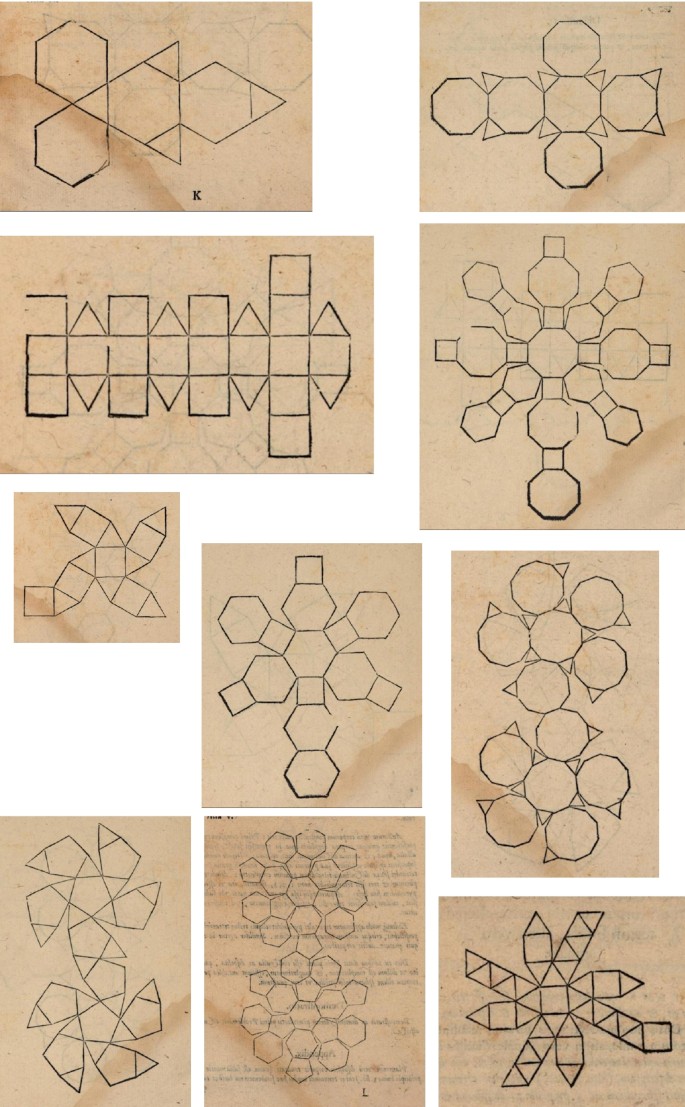
Figure 17 shows the planar nets drawn by the Anonymous Author for ten Archimedean Solids (the snub dodecahedron has an extra pentagonal face). Individual nets of the truncated cube, the rhombitruncated cuboctahedron and the rhombitruncated icosidodecahedron are missing, but their faces are shown within the planar nets of other solids. Figure 18 shows the nets of the cube and the octahedron with an inscribed truncated cube (left) and rhombitruncated cuboctahedron (middle and right).

In 24 woodblocks, the Anonymous Author drew the faces of the thirteen Archimedean Solids inside the net of specific Platonic Solids. The fact that other than the convex regular are inscribed inside the Platonic Solids is a remarkable development of the apocryphal Book XV of the Elements. The only author we found who, at the time, investigated (two) Archimedean Solids inside the Platonic and vice versa, was François de Foix-Candale (1512–1594). Studies on the Platonic Solids inscribed in each other are known since at least the fifth or sixth centuries, when the author of Book XV would have lived. In the fifteenth century, Piero discussed his conclusions on the subject in Part III of the Libellus (and, subsequently, Pacioli, at the beginning of the Tertius Tractatus in Divina Proportione). Nicolo Tartaglia (1560a; b), an Italian mathematician who lived between 1500 and 1557, studied the regular bodies inscribed in each other in Parts IV and V of the General Trattato Di Numeri, Et Misure, which were published in 1560.^{Footnote 46}

François de Foix-Candale, in “Liber Decimusquintus” of his Elementa Geometrica, first published in 1566, presents twenty cases of Platonic Solids inscribed in each other, all of which are conveniently illustrated, except for the tetrahedron and the cube inside the icosahedron, which Foix-Candale (1578, p. 457) explains only in writing. Foix-Candale proposes three additional books to the medieval version of the Elements.^{Footnote 47} “Liber Decimusseptimus” is particularly interesting because it begins with a definition of the “exoctaedron” and the “icosidodecaëdron”, after which Foix-Candale (1578, pp. 507–536) discusses how each of the Platonic Solids can be inscribed in them and how each can be inscribed in a Platonic Solid, as well as in each other. Figure 19 shows the drawing with which Foix-Candale (1578, pp. 530–531) illustrates the octahedron inside the icosidodecahedron and our interpretation on the side.

Foix-Candale does not seem to be the Anonymous Author, given that he does not describe other Archimedean Solid besides the cuboctahedron and the icosidodecahedron, nor does he display any solid body in planar nets, despite the complexity of some perspective drawings. In a subsequent section, we share our preliminary conclusions about the identity of the Anonymous Author, whom we believe could neither have been Albrecht Dürer nor Johann Tscherte. We also discuss our interpretation of the hatched patterns in some planar nets, that we believe were designed with a specific purpose. The Anonymous Author determines the vertices of all the Archimedean Solids on the faces of the Platonic Solids with precision, revealing an unparalleled depth of geometrical knowledge that becomes all the more intriguing in the few planar nets in which a third solid body seems to be shown inside other two.

None of the planar nets in the woodblocks display auxiliary lines to explain how the vertices were determined, yet the procedure to obtain the more complex bodies is far from trivial: no drawings of the snub dodecahedron were known before 1619, let alone how to enclose it inside the dodecahedron or the icosahedron. Even if the Anonymous Author somehow had access to Pappus’ Synagoge (which only describes the number and configuration of the faces in the bodies discovered by Archimedes), developing a systematic study of these solid bodies, some of which were unknown at the time, on the nets of the Platonic Solids with such surprising accuracy and so differently from anything else in his time, is truly remarkable. With very few exceptions, all the solid bodies have regular faces and the vertices are accurately determined.^{Footnote 48} These and other brilliant conclusions are given in planar nets for us to build, taking even further the new knowledge of building paper models out of planar nets that Dürer had initiated a few years back and Hirschvogel continued.

Figure 20 shows a virtual simulation of how the models in Figure 18 would look like if the nets were printed in a dark paper and some faces folded. The truncated cube on the left is one of the few exceptions in which the inscribed body is non-uniform because the edges of the cube were divided into three equal parts instead of the ratio 1: square root of 2 : 1. On the remaining woodblocks, the vertices are in their exact location or very close. Instead of obtaining models of the enclosed bodies (which had been given in Figure 17), these nets are meant to visually explain how the irregular bodies derive from the regular. Although meant to be instructional, the truth is that to someone unfamiliar with the subject, such planar nets and models are less helpful than one would think. The bodies meant to be shown are understandable when the net of the Platonic body is folded, but imagining a solid body inside a paper model from what could be a projection of its edges may be difficult without an idea of the enclosed body.

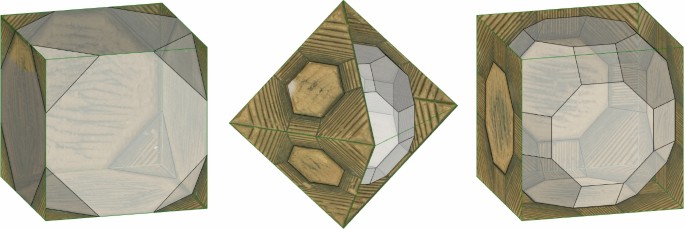
Figure 21 shows the only woodblocks with Archimedean Solids inside the net of the octahedron: the snub cube, the cuboctahedron, the rhombitruncated cuboctahedron and the truncated octahedron. The sets of faces that share the same planes as the faces of the octahedron are unmarked, while the remaining have different hatched patterns. The triangles in the net at the bottom right, which become the square faces of the truncated octahedron, have a dark hatched pattern to indicate that the corners of the octahedron are not part of the resulting body. A new face with a specific orientation emerges if we truncate each vertex. If we were to fold these dark triangles on a paper model, they would have to overlap to roughly materialize the squares. The lines in the pattern on those that become square and octagonal faces in the snub cube (upper left) and the rhombitruncated cuboctahedron (bottom left), respectively, are not parallel to the delimiting edges. They might have been carved this way because it was an easier solution. However, our analysis of the gradient pattern in these and similar cases led us to believe they may stand for augmentations or concavities performed on the octahedron with which a different solid is obtained. On the other hand, they might also be meant to unveil another solid body inside the other two, as we will later show.

2.6 Wentzel Jamnitzer

Wentzel Jamnitzer (1507/08–1585) is one of the most important representatives of the Mannerism period in Nuremberg and was considered, in his time, one of the best German goldsmiths, according to Flocon (2006, p. 18). He was born in Vienna and lived in Nuremberg from 1543 until his death in 1585. Jamnitzer crafted several scientific instruments, one of which turned Dürer’s window into a portable device with a mobile pin replacing its frame. The etching by Jost Amman (1539–1591) in Figure 22 portrays Jamnitzer using one of such perspective devices^{Footnote 49}. Amman was a prolific artist who moved to Nuremberg in 1560 and worked with Jamnitzer in the reproduction of his drawings on the copper plates^{Footnote 50} used for printing Perspectiva Corporum Regularium. The book was published in 1568 and includes 164 astounding drawings of solid bodies that Jamnitzer obtained from the Platonic Solids “by augmentation, truncation, cutting notches into the sides or faces, or some combination of these, all done in a regular manner” as Cromwell (1997, p. 130) denotes.

In the first part of the book, Jamnitzer includes a sub-chapter^{Footnote 51} for each Platonic Solid with a title page and 24 drawings: six per Plate, the first being the regular body. Apart for the tetrahedron, all the Platonic solids (and a few others) are shown twice in different positions. The subtitle pages bear the initials J and A, which stand for the signature of Jost Amman.^{Footnote 52} In the second part of the book, four other drawings for each regular body exist, along with twelve variations of the sphere, eight variations of the cone, and four variations of toroidal forms that may be interpreted as mazzocchi. When Jamnitzer describes his geometrica corpora, he mentions the number of vertices, edges and faces of the regular body without explaining how the remaining were obtained. Jamnitzer may have decided not to include such details because, contrary to Dürer, Hirschvogel or Barbaro, he did not mean his book to be instructional, but a testimony of his geometrical knowledge, exuberant creativity and mastery of perspective drawing. The only explanation regarding how the complex forms are obtained is given when Jamnitzer (1568, Plate A.VI) introduces the octahedron in the subtitle page, shown in Figure 23:

AER. The air.

OCTAEDRON.

Solidum octo basium triangularium.

A diamond point / or body made of eight triangular planes.

The other body is composed of eight equilateral triangles / has twelve edge corners, twenty-four plane angles / which make six solid corners / from this body as base / by cutting off and putting on [parts] to anyone’s liking / Henceforth, 23 other different solids are shaped / and drawn.^{Footnote 53}

In the Prologue, Jamnitzer (2006, pp. 67–68) says he decided to bring forth his experience of many years investigating the art of perspective and show the advantageous and practical method that he invented and has not found anywhere else. With perspective, he adds, any object, seen from afar, is represented according to its geometry with such an accuracy that it will seem impossible that the drawing was made by hand. With no intention of praising his Perspectiva or himself above others or diminishing their work, Jamnitzer (1568, Prologue, third page) adds, he will demonstrate the art of perspective with an easy and pleasing method that, contrary to what is usually taught, avoids all deviations and unnecessary lines or points:

So please, dear friendly reader / you may take in my cordial, good opinion, true to my diligence / and once I feel gratitude / I am instigated / to let the other part of my related work / come out as well. Because even though I was willing / to loyally bring out the whole work at once / and have it printed / due to other of my business / and work duties, it could not be prepared and ordered in the copper this time together [with the first book] / however / the mentioned other part / shall come to light through means of Godly grace, for the benefit of all.^{Footnote 54}

Explanations about this method, however, are nowhere to be found^{Footnote 55}. Jamnitzer says he is considering publishing a second book upon the acceptance of the first since it was impossible to include all that he had wished while the book was being produced. Such a project, however, does not seem to have ever been accomplished. Jamnitzer died 17 years after the publication of Perspectiva Corporum Regularium.

Kemp (1992, p. 64) tells us that Jamnitzer left no explanations about how his drawings, whose parallel lines decidedly converge to distant points, were made, and notes that “his geometrical drawings which have survived show no signs of constructional lines of the kind necessitated by the Piero–Dürer and other methods”. In the opinion of Kemp, this suggests that Jamnitzer used an instrumental method to describe his polyhedral forms. Kemp notes that it is rather unlikely that his more intricate forms were manufactured or even studied individually as physical models. Andersen (2009, p. 228) suggests that Jamnitzer used perspective instruments to measure distances from points on real objects to draw them in perspective. We believe such objects would have been three-dimensional models of basic solid bodies built from planar nets introduced by Dürer and Hirschvogel, whose work Jamnitzer definitely knew well.

Without underestimating Jamnitzer’s genius and the inventiveness of his beautiful creations, if we compare certain drawings in the first part of the book, we see that some vertices derive from the division of the edges in other drawings, which means that Jamnitzer did not need to craft all of them as three-dimensional models. It would have been enough to craft a few basic models and locate construction points in their edges that would act as guidelines to draw different models. The rhombicosidodecahedron in Figure 24 might be such an example because its pentagonal faces may be obtained with the division into three equal parts of the edges of the dodecahedron immediately above it. This does not mean that conceiving each of these objects gets necessarily easier, far from it. Without the limitations of the material world, the mind is free to imagine even more unusual and extraordinary objects. Jamnitzer proves us that he masters the art of drawing whatever complex forms he imagines and he does it so convincingly that, as Jamnitzer himself tells us, everyone will think they are actually there and we can almost touch them (2006, p. 67).

Many fabulous polyhedra are beautifully illustrated in this book, but here, we restrict our attention to the nine Archimedean Solids that Jamnitzer drew. Figure 24 shows the truncated tetrahedron, the truncated octahedron, the cuboctahedron, the icosidodecahedron and the rhombicosidodecahedron, as well as the rhombicuboctahedron and the rhombitruncated cuboctahedron, in non-uniform versions. Most of these solid bodies are illustrated on other Plates, whether in different positions, combined with other forms, or serving as guidelines to others. Jamnitzer drew the truncated icosahedron in Plate D.II, encircled by a light structure with a set of vertices coinciding with those of a dodecahedron. A non-uniform version of the truncated cube is in the base of one of the sculptures in Plate G.II, on the second part of Perspectiva Corporum Regularium.

2.7 Daniele Barbaro

Daniele Barbaro (1514–1570) was a humanist, diplomat, and architect born in Venice who is mostly known for his writings on architecture, especially the translation and commentaries on Vitruvius’ treatise. His last book, La Pratica della Perspettiva, is a treatise on perspective drawing meant for painters, sculptors, and architects, as stated by Barbaro (2021, p. xiii) himself. Published between December 1568 and January 1569,^{Footnote 56} it was the first book on linear perspective to be printed in Italy.

Field (1997, p. 244) notes that Barbaro was the author who described more Archimedean Solids in the sixteenth century. If our conjecture on the identity of the author who conceived the nets in the woodblocks is confirmed (or their authorship traced to another person who would have been active before 1568), this perception may change. Barbaro described eleven Archimedean Solids, including the rhombitruncated icosidodecahedron, which neither Dürer nor Hirschvogel had included in their books. The rhombicosidodecahedron, as we have seen, had been described by Hirschvogel in 1543. The Anonymous Author, on the other hand, determined the vertices of the thirteen Archimedean Solids on planar nets of the Platonic Solids.

The studies that Barbaro did for his treatise are undeniably rooted in the knowledge of his time, so much so that he recognizes the studies of Piero the painter, as well as those of Dürer an excellent man, as bases for his own in La Pratica della Perspettiva. The influence of Piero transpires on the occasional overlapping of Barbaro’s writings with Piero’s, to whose manuscript Barbaro had access from the copies circulating in Venice at the time.^{Footnote 57} Many similarities exist between the treatise of Barbaro and Underweysung der Messung. Curiously, Barbaro did not include Dürer’s snub cube in his treatise, and we will later discuss a possible reason for this omission. But regarding his studies on solid geometry, Barbaro (1568, p. 3) acknowledges no influences and even criticizes Piero for his studies on the subject while, at the same time, he praises the findings of Dürer:

Perhaps we should not call precepts, and rules, to some light practices that have been placed without order, and foundation, and are rudely explained: in these are also some of Piero dal Borgo S. Stefano, and others, which for idiots we can use.^{Footnote 58}Few things has left us Alberto Durero, although ingenious, and accurate.^{Footnote 59}

Barbaro may have been influenced by Hirschvogel, given the popularity of the book Geometria that, according to Andrews (2022, p. 114), was “still in use at least 100 years after its publication”. There are evident similarities between the treatise of Barbaro and the work of the Anonymous Author that we will later show. As to the influence of Jamnitzer’s Perspectiva Corporum Regularium, which was published a few months before La Pratica della Perspettiva, Field (1997, p. 271) finds it possible “but not very likely” that Barbaro knew it in printed form, although, Field adds, he might have known a manuscript version. The difference in their approaches leads us to believe that, if there ever were any influences from Hirschvogel or Jamnitzer in Barbaro, the former would have been much more significant than the latter. Jamnitzer’s approach to polyhedral forms is more artistic, and very different from Hirschvogel, the Anonymous Author or Barbaro. His purpose, rather than explaining how his fabulous new forms were conceived or drawn, was to exhibit his luxuriant creativity and mastery in perspective drawing.

Besides the mazzocchio and its variations, Barbaro describes 39 corpi sodi in La Terza Parte of his treatise: a triangular pyramid, the convex regular polyhedra, eleven Archimedean Solids, nine convex non-uniform polyhedra,^{Footnote 60} and thirteen concave polyhedra derived from the augmentation of other polyhedra (eight of which had been described by Pacioli and Leonardo). For each case, with the exception of the first pyramid and the mazzocchio, Barbaro presents a planar net that he names spiegatura. Every regular body is described, as Barbaro (1568, p. 45) states, with a “pianta perfette” or perfect plan; a “digradate” or degraded, determined from the perfect plan; and “i dritti” and “loro adombrationi”, a drawing rendered with shadowing^{Footnote 61}. The perfect is a plan or orthographic projection; the degraded, an elevation in parallel perspective.^{Footnote 62} Apart from the “adombrationi”, every perspective drawing in La Terza Parte is shown in wire-frame mode with all the edges in the same thickness. As mentioned earlier, Barbaro (1568, pp. 60, 65) only uses different line types in two drawings, to distinguish the cuboctahedron and the rhombicuboctahedron from the cube from which they derive. Figure 25 and Figure 26 illustrate the spiegature of the eleven Archimedean Solids that Barbaro describes.

Barbaro introduces Chapters VII to XIV as irregular bodies that are born from the regular bodies, while the remaining are another body or another irregular body born from a compound body. The expression used by Barbaro (1568, p. 88), “corpo il quale nasce da uno corpo composto”, does not refer to a polyhedron compound, as he could not possibly have had interpenetrated polyhedra in mind. A body born from a composto means it has not derived from a regular body but from another one, itself derived from a regular body. Four spiegature in Figure 25 and Figure 26 are not entirely accurate: the cuboctahedron has an additional triangular face; the rhombicuboctahedron has a rectangular face instead of squared; the truncated octahedron has a hexagonal face where a squared one should be; and a triangular and a squared face are missing in the rhombicosidodecahedron. In addition to the spiegature, many Archimedean Solids are shown with two drawings in parallel perspective, each standing in a different type of face. The truncated dodecahedron in Figure 27 is an example. For the truncated tetrahedron, the rhombitruncated cuboctahedron and the rhombicosidodecahedron, only one degraded is shown. The rhombitruncated icosidodecahedron is only shown with a partial net, probably because it never got to be built as a three-dimensional model.

Barbaro explains how Chapters VIII to XV, XVII and XXI are obtained from suitable truncation of the vertices of another body, after dividing its edges into specific parts. He also declares the cuboctahedron is derivable from the cube and the octahedron, similar to the icosidodecahedron, that derives from the dodecahedron and the icosahedron. Field (1997, p. 271) notes that Barbaro was the first to recognize this. The Anonymous Author, presumably earlier, had reached the same conclusion not only regarding the cuboctahedron and the icosidodecahedron but also in relation to far more complex cases.

The operations with which Barbaro explains how the cuboctahedron, the truncated octahedron, the icosidodecahedron, and the truncated icosahedron are obtained are in precise alignment with the conclusions by Piero, Pacioli/Leonardo and Dürer. The truncated tetrahedron, however, is succinctly explained as the body formed of four surfaces of six sides and four triangles with equal sides being born from the pyramidal body.^{Footnote 63} The procedures for the truncated cube and rhombicuboctahedron are correctly explained. Regarding the truncated dodecahedron, the explanation Barbaro (1568, p. 76) gives is not fully correct because the division of the edges of the dodecahedron into three equal parts, “partendo i lati del dodecaedro in tre parti eguali”, does not produce regular faces alone. The same concerning the explanations on the rhombicosidodecahedron, rhombitruncated cuboctahedron and rhombitruncated icosidodecahedron. Even so, the two perspective drawings of the truncated dodecahedron are mostly precise, as Figure 27 shows. From these and similar drawings, we conclude that Barbaro deduced his conclusions while observing three-dimensional models that had been crafted from planar nets with regular faces. If he had used planar nets derived from the incorrect division of regular faces, the perspective drawings would not have been as precise as they are.

An interesting case is the truncated cube in Figure 28. To draw its perfect, Barbaro explains how an octagonal face is obtained: two squares with their angles at equal distances, bcde, fghi, form the said surface of eight sides.^{Footnote 64} Regardless of a missing edge and two vertical faces that do not quite seem to be octagonal, the degraded of the second body born from the cube is very close to our axonometric representation on the right. Barbaro also shows the truncated cube standing on a triangular face, but the degraded in Figure 29 has many inconsistencies compared with a similar axonometric representation. In the perfect, Barbaro assumes the outline is a dodecagon with vertices on the two surfaces of six unequal sides bcdlkp and ghimef, equidistant from each other.^{Footnote 65} Williams and Monteleone (2021, p. 212) have interpreted this perfect as an adaptation of the “construction from the design of the Roman Theatre based on 4 squares in the circle” that the authors assert Barbaro certainly knew.

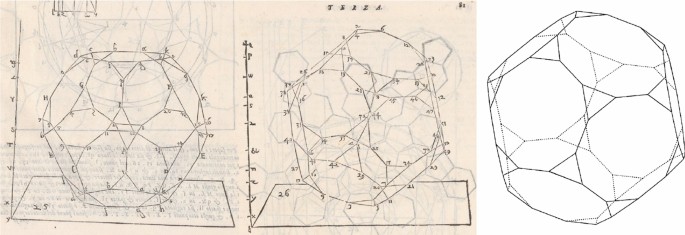
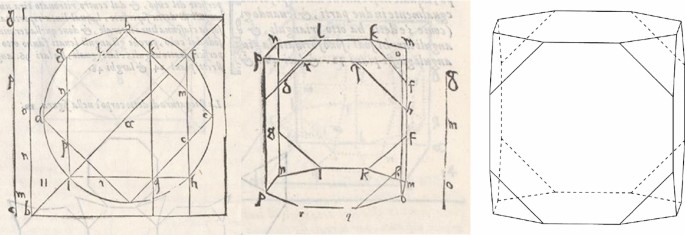
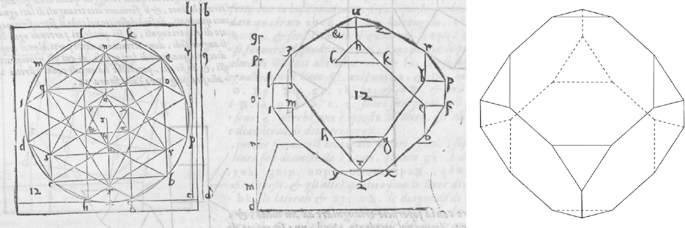
Figure 30 illustrates that each set of vertices that Barbaro assumed to outline a square, in fact, outline a rectangle. The difference, however, is practically insignificant: in a truncated cube with edge 10 and two triangular faces in the orientation of plane xy, each set of 4 vertices outline a rectangle 26,131 24,142 that projects in xy as 25,485 x 24,142. This detail alone, of course, does not justify the problems in the degraded, but examining a model of the truncated cube in such an unusual and difficult to draw position and arriving at these conclusions is revealing of Barbaro’s originality and insightful curiosity.

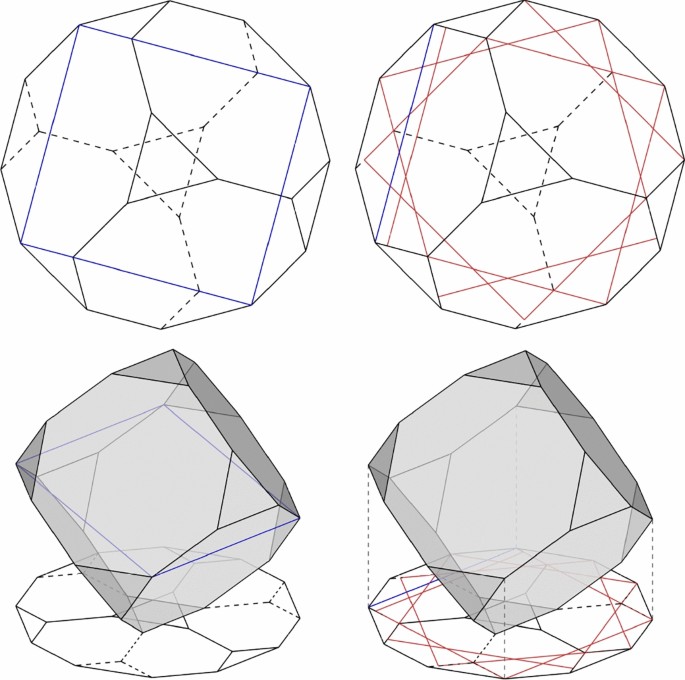
Regarding the inaccuracies in the graphic descriptions of La Pratica della Perspettiva, it should be emphasized that Barbaro may not have been directly responsible for all, even if, according to Field (1997, p. 271), the draughtsman who was assisting him in the production of his treatise “simply made faithful copies of the drawings he was given”. Barbaro was aware that it might not always be so, and a clear sign of this is when, having understood how imprecise the degraded of the second irregular body that is born from the cube (Figure 29) would be, Barbaro warns the reader at the end of its explanation by mentioning the person who was assisting him, denoting that “the error of the engraver in figure 12 will be corrected with the rules that have been given”.^{Footnote 66}

With the noteworthy exception of the Anonymous Author, the way in which Barbaro discusses solid geometry concepts is different and more complex than his predecessors since he meticulously explains (although not without flaws) how to obtain each orthographic projection and perspective drawing on most of the solid bodies he describes. Barbaro shows many of these in different positions, some recognizably difficult to draw in perspective, and introduces nine non-uniform polyhedra, most of which were unkown before 1568. His contribution to the history of polyhedra is coherent and systematic and one of the most significant in the sixteenth century.

2.8 Lorenz Stöer

Lorenz Stöer was a highly productive artist who drew numerous polyhedral forms, many inside others and others still in strange architectural settings. Jamnitzer’s influence is evident in many solid bodies. Still, those unknown at the time and different from Perspectiva Corporum Regularium may have been adapted from Jamnitzer’s drawings that had not been included in his book or from another author. Stöer himself may have also discovered these new forms.

Stöer was born in Nuremberg before 1555 and moved to Augsburg in 1557, where he came to die sometime after 1599. In 1567, Stöer (1567) published eleven prints under the title Geometria et Perspectiva. According to Wood (2003, 249), all seem to have been drawn freehand before printing. No Archimedean Solids are described in these prints, only on the title page, in a form composed of a cube and a cuboctahedron. Stöer also drew a cuboctahedron, in Leonardo’s style, on the cover page^{Footnote 67} for Geometria et Perspectiva that is shown in Figure 31.

In the upper right corner of Figure 31, Stöer drew a rectified truncated octahedron, which is obtained by truncating the vertices of the truncated octahedron in the edges’ midpoints. There are drawings of a similar solid body in two books published the year after Geometria et Perspectiva: Perspectiva Corporum Regularium and La Pratica della Perspettiva. Jamnitzer (1568) shows the rectified truncated octahedron in Plates B.II and B.IV, while Barbaro (1568) describes the “corpo di sei quadrati, e otto hexagoni” in pages 90–93, with a spiegatura, a perfect, and a degraded. Assuming the cover in Figure 31 was printed before 1568, Stöer would have described the rectified truncated octahedron before Jamnitzer. However, we do not know much about how the artists that were active in Nuremberg worked with each other. Stöer could have known Jamnitzer’s book while it was still in a manuscript version or vice-versa, Jamnitzer could have known Stöer’s works^{Footnote 68}.

From around 1562 to 1599, Stöer explored the Platonic and Archimedean Solids and many other polyhedral forms in 336 exuberant watercolours, that, according to Wood (2003, p. 276), could have been designed as intarsia motifs. They were never published in printed form and were compiled in a specific sequence by someone who has not been identified. Bound together around 1600^{Footnote 69} under the title Geometria et Perspectiva Corporata et Regulata, the watercolours were in the possession of the library of the bishop of Freising in 1696, coming to the University Library of Munich in 1826.^{Footnote 70}

There are eleven Archimedean Solids in these watercolours,^{Footnote 71} some of which in non-uniform versions, drawn individually or in peculiar arrangements with or within other solid bodies. Figure 32 shows the truncated cube, cuboctahedron, rhombicuboctahedron, truncated tetrahedron, truncated octahedron, icosidodecahedron, truncated dodecahedron, rhombitruncated icosidodecahedron, rhombicosidodecahedron, and truncated icosahedron. The last watercolour in Figure 32 shows a solid body with augmentations on the hexagonal and rectangular faces of a non-uniform rhombitruncated cuboctahedron. In many watercolours, certain solid bodies might have been intended as regular-faced, but their drawings do not depict them as such.

Stöer announced in 1555 that he would publish a second book, but he never accomplished such a project. Possible reasons may have been the impossibility of finding a noble patron to support the publication, Stöer concluding that his work was not original enough, or that he was not sufficiently organized to accomplish the project, as suggested by Wood (2003, p. 246), who adds that Stöer may never have “intended any such thing.” Even if we never get to discover Stöer’s intentions, his inventiveness certainly deserves a closer look.

2.9 Rafael Bombelli and Simon Stevin

Our survey on the systematic treatments of Archimedean Solids in the sixteenth century would not be complete without the mathematicians Rafael Bombelli and Simon Stevin, who strongly influenced the academic development of mathematics. Stevin, according to Andersen (2009, pp. 269–289), was also important to the development of perspective theory in the Netherlands.

Rafael Bombelli (1526–1572) wrote the treatise L’ Algebra, which was published in 1572. Bombelli intended to publish other volumes in addition to Books I, II and III, but that would not occur during his lifetime. In 1923, the historian of mathematics Ettore Bortolotti (1866–1947) discovered the manuscript B 1569, with additional studies that Bombelli had developed, in the Archiginnasio Library in Bologna. In 1929, Bortolotti (1929) edited and published these as L’ Algebra Opera di Rafael Bombelli da Bologna Libri IV e V Comprendenti “La Parte Geometrica” Inedita. The part that Bortolotti (1929, p. 23) names Libro Quinto deals with the application of algebra to geometric problems and finishes with a description of the five regular and three semiregular bodies, all of which are illustrated with planar nets. Figure 33 shows the nets of the octahedron, as well as those of the truncated tetrahedron, cuboctahedron and truncated cube, which Bombelli/Bortolotti (1929, pp. 293, 296) respectively name as “Tetraedro Tronco”, “Cubottaedro” and “Cubo Tronco”. The nets of the cuboctahedron and the truncated cube are strikingly different from others we have seen until now. The net of the truncated tetrahedron, on the other hand, is the same as the Anonymous Author and Barbaro. The same happens with the net of the octahedron, as we will later show.

Before explaining how the octahedron and the truncated tetrahedron are obtainable from the tetrahedron, Bombelli/Bortolotti (1929, p. 293) note that other bodies with equal edges are obtainable from the regular ones, the majority of which have different faces, depending on how the edges are divided:

Of the above five bodies, an infinite number of equal sides are born and of equal solid angles, but not of similar surfaces, because (…) those which have similar surfaces cannot be other than five. Of these five, by cutting their angles in two ways, other bodies of equal sides will be born, and the majority with dissimilar surfaces.^{Footnote 72}

Bortolotti (1929, p. 302) says there is no certainty whether Bombelli ever developed any other studies on the semiregular solids or if these were lost. Given his different contribution to the subject, it would have been interesting to know any other conclusions Bombelli might have arrived at.

Simon Stevin (1548–1620) wrote Problematum Geometricorum^{Footnote 73} that was published in 1583 and includes the ten Archimedean Solids shown in Figure 34. The subtitle in which they are presented is Third Book on the description of the five Regulars, five augmented Regulars and nine Truncated regular bodies, inscribed in the same sphere.^{Footnote 74} We have translated the word “auctorum” in the subtitle to augmented, even though a direct translation would be author because, in Medieval Latin, it would also have meant the one who gives increase^{Footnote 75}.

In “Definitiones quinque auctorum corporum regularium”, Stevin (1583, p. 49) explains that adding a tetrahedron to the faces of a regular body produces five augmented new ones. Similar to Dürer, whose treatise Stevin knew, he does not illustrate them. In 1509, Pacioli introduced these concave deltahedra in Divina Proportione and Leonardo drew them in solidum and vacuum modes. If Stevin knew Divina Proportione, he may have decided to name them “auctorum” to distinguish his studies from Luca Pacioli, who used the term “elevatum”.^{Footnote 76} These augmented bodies are not mentioned collectively by any name in Underweysung der Messung nor in its translation into Latin by Joachim Camerarius.^{Footnote 77} In 1568, Barbaro (1568, pp. 105–107) includes planar nets for these augmented bodies in La Pratica della Perspettiva, also without giving them names. Since the nets were difficult to interpret, Barbaro numbers every face to explain how to assemble each model.

Of all the sources Stevin might have had for his studies on solid geometry^{Footnote 78}, the first edition of Underweysung der Messung or its translation into Latin are the most evident since the augmented and truncated bodies are the same as Dürer, as well as their planar nets (Cf. Figure 12 with Figure 34). The one missing is the solid body that Dürer did not describe in 1525, the truncated dodecahedron. The net that Stevin presents is an adaptation of the net Dürer had drawn for the dodecahedron. In Definitiones 12–22, Stevin (1583, 50–54, 73–83) describes nine Archimedean Solids as “truncatorum corporum regularium”, the truncated version of the regular bodies adding, in some cases, short notes. Their planar nets are shown in Distinctiones 11–19. After Definitio 22, Stevin presents a series of problems discussing the circumsphere that contains the vertices of the bodies he described, after which he summarizes his conclusions with a list of names and line segments to compare the diameter of the “circumscriptibilis sphera” with the edge length of each solid body. Similar to the augmented bodies, Stevin (1583, p. 46) proposes names for the truncated bodies because he has found no one who had done it before:

…we could not find the origin or the names of such bodies in anyone, but we thought they should not stand without a certain foundation, then we saw that those derived from the regular bodies were many, for one of them was a truncated tetrahedron, another three, were truncated cubes, and the fifth, a truncated octahedron: the truncation of the sixth body was unknown to us who write this, but we do not doubt that it had its origin in the truncated cube.^{Footnote 79}

The sixth body that Stevin mentions is the snub cube, which Dürer also had named “Sechste Corpus”. Stevin treats it separately from the other truncated bodies. More complex than the names Kepler would choose decades later, Stevin’s terminology for the truncated bodies^{Footnote 80} is meant to explain how each is obtained from another. The last words in those resulting from the division of the edges of a regular body into two equal parts are “per laterum media”, which means the vertices were truncated in the edges’ midpoints. Those in which the edges are divided into three equal parts finish with “per laterum tertias” because the edges were split into thirds. For those in which the edges were divided into three unequal parts, the last words are “per laterum divisiones in tres partes”. Stevin names the rhombicuboctahedron and the rhombitruncated cuboctahedron as “bitruncatus cubus primus” and “bitruncatus cubus secundus”, and explains how to obtain them in Definitiones 15 and 16, respectively, from the division of the edges of the cube into three and five unequal parts. Stevin (1583, p. 47) declares to have discovered three new bodies in Definitiones 20, 21, and 22: the truncated dodecahedron, the icosidodecahedron (obtained from the icosahedron), and the truncated icosahedron, yet denoting that:

If by chance they had been discovered by another one before us (of which we almost have no doubts, owing to the great diligence of the ancients in the search for forms), let us declare that we were ignorant about this. As such, we announce such facts in defence of our invention.^{Footnote 81}

The “truncatum dodecaedrum per laterum media” and the “truncatum icosaedrum per laterum media”, respectively treated in Definitiones 19 and 21, are icosidodecahedra. In additional notes, Stevin recognizes that Definitiones 19 and 21,^{Footnote 82} are the same (as well as the cuboctahedra, treated in Definitiones 13 and 17). The fact that Stevin declares the [truncatum] “icosaedrum per laterum tertias” or truncated icosahedron as his discovery, confirms that he was not studying the posthumous edition of Underweysung der Messung. Otherwise, he would have known that Dürer had described it, as well as the icosidodecahedron. Before Dürer, we recall, Pacioli had described the icosidodecahedron and Piero, the truncated icosahedron. Leonardo and Barbaro also described the truncated dodecahedron. Stevin devises the icosidodecahedron from the icosahedron but Barbaro, in La Pratica della Perspettiva, which Stevin does not seem to know, had mentioned this 15 years earlier and, before him, the Anonymous Author. In the Appendix, Stevin (1583, pp. 82–83) addresses the snub cube a second time:

In reality, the arrangement of the planes of the truncated body (of which mention was made at the beginning of this Book 3), of whose method of truncating I was not aware when writing these facts, is as follows: Let be arranged, as shown below, six squares and 36 triangles. But because of our unawareness of how the truncation occurred and its true origin, we could not build this geometric body inside a sphere as we did to the other bodies.^{Footnote 83}

Stevin mentions the sixth solid body, but he admits that he could not determine the diameter of its circumsphere and that he does not know how this solid body is obtained. This was also probably why Barbaro did not include the snub cube in his treatise.

2.10 Summarizing consistent studies on the Archimedean Solids of the 15^th and 16^th centuries

Table 1: Systematic studies on the Archimedean Solids in the 15^th and 16^th centuries

Table 1 summarizes our analysis of the studies on the Archimedean Solids in the fifteenth and sixteenth centuries that were more consistent and systematic. This analysis is not exhaustive since our survey for historical descriptions of the Archimedean Solids (and polyhedra in general) is ongoing. Some drawings in these studies depict non-uniform versions of Archimedean Solids, but the Table does not identify which ones, as this was mentioned before. The horizontal sequence in which the Archimedean Solids are listed in the Table matches the degree of complexity in obtaining them.^{Footnote 84}

Authors of the fifteenth and sixteenth centuries who described only a few or no Archimedean Solids have not been included.^{Footnote 85} We also did not include La Pratica di Prospettiua by Lorenzo Sirigatti (1596, pp. 61, 64 Libro Secondo) in our study (although Sirigatti drew the truncated octahedron, the cuboctahedron, the rhombicuboctahedron, the icosidodecahedron and a non-uniform truncated icosahedron), because the book was published near the end of the sixteenth century. We also omitted De varia commensuracion para la esculptura y architectura (1585, 33–42) by Juan de Arfe y Villafañe (1535–1603), because the drawings of the Archimedean Solids are copies of Hirschvogel’s drawings without most of the auxiliary lines.^{Footnote 86} Villafañe did not include the rhombicosidodecahedron in his book, probably because he only focused on the solid bodies to which Hirschvogel presented complete descriptions.

In 1619, Johannes Kepler (1619, pp. 47–66) published a description of the thirteen Archimedean Solids in Book II of the Harmonices Mundi.^{Footnote 87} In the opinion of Field (1997, p. 269), the fact that Kepler does not credit any sources for his findings may derive from his recognition that Dürer would have described them all if he could.^{Footnote 88} Kepler knew Underweysung der Messung and even cited it (1619, p. 39) but not in relation to solid geometry. Kepler may have also known Divina Proportione and La Pratica della Perspettiva, but if he did, he probably underestimated them.^{Footnote 89} Regarding Hirschvogel and Stöer, Andrews (2022, p. 209) tells us that the University of Tübingen, Kepler’s alma mater, acquired Geometria and Geometria et Perspectiva, but we do not know if Kepler knew any of these books. Johannes Kepler was an absolute pioneer in his scientific creativity, and his work is essential to the history of polyhedra, but while most of the authors we discussed were rediscovering the irregular bodies by themselves or with very little background material to work on, Kepler based his conclusions on the Archimedean Solids on their configuration described by Pappus in the Synagoge, whose translation into Latin was published in 1588.

3 Drawing from models and modelling from nets

Many images of solid bodies from the late fifteenth and early sixteenth centuries were undoubtedly drawn from observing three-dimensional models^{Footnote 90} but due to their fragility, none arrived at our age. Pacioli (1509, folio 22, Pars Prima) speaks about such three-dimensional models when he tells us that his poverty does not allow him to use other than materials of inferior quality, de vil materia, to make the models he believes would be worthy of the most precious metal and gemstones, de pretioso metallo e fine gemme.

In the Portrait of Luca Pacioli attributed to Jacopo de Barbari, Pacioli is portrayed with another person^{Footnote 91} and, among other items, a glass model of a rhombicuboctahedron drawn in parallel perspective, finely painted and reflecting a nearby window (Fig. 35). Comparing it with Fig. 8, we notice that the position in which the rhombicuboctahedron was drawn is substantially different from the one in Divina Proportione. Moreover, it does not show an evident relation, in terms of perspective, with the rest of the picture. According to Séquin and Shiau (2018, p. 28), the depiction of what would be reflected on the surface of this rhombicuboctahedron has several flaws that indicate the artist may not have been observing a glass container of such dimensions, suspended and half-filled with liquid. The authors suggest that this rhombicuboctahedron was sketched separately from the painting, perhaps from a smaller model or a geometrical construction, before being copied onto the canvas, which strengthens our perception that the original drawing was done while observing a physical model from above and very close to the observer, most likely in the artist’s own hands.

If Pacioli and Leonardo studied solid bodies from physical models, there had to be a method to craft them; otherwise, making new ones would not have been possible. Some of the bodies Leonardo drew would have been extremely difficult (if not impossible) to carve or sculpt directly from wood or a block of stone without a model to follow. Conceiving solid bodies that were unknown at the time would also have been complicated. Pacioli, we recall, was the first to describe the rhombicuboctahedron after Archimedes.^{Footnote 92} The act of assembling polygonal-shaped paper or cardboard panels to materialize a three-dimensional form in the late fifteenth and early sixteenth centuries, even if unstable or imprecise, may not have been unknown to those who studied solid geometry more seriously. References to adjoining polygonal shapes can be recognized as early as in the Timaeus, when Plato describes how the cube is formed by assembling six squares from four isosceles right triangles:

Now the first of the elemental triangles ceased acting when it had generated these three solids, the substance of the fourth kind being generated by the isosceles triangle. Four of these combined, with their right angles drawn together to the center, produced one equilateral quadrangle; and six such quadrangles, when joined together, formed eight solid angles, each composed of three plane right angles; and the shape of the body thus constructed was cubic, having six plane equilateral quadrangular bases.^{Footnote 93}

According to Friedman (2019, pp. 83–85), Pacioli was the first known author to explore folding paper as a mathematical procedure in De Viribus Quantitatis, an unfinished manuscript on recreational mathematics that he wrote with Leonardo.^{Footnote 94} But if Pacioli ever folded pieces of paper or assembled polygonal-shaped plaques in wood or cardboard to build three-dimensional models, he abstained from mentioning it in Divina Proportione. Friedman (2019, pp. 49–50) mentions a net of the regular dodecahedron from the book Dürers Gestaltlehre der Mathematik und der Bildenden Künste. According to Max Steck, the author of this book, Leonardo drew the net shown in Fig. 36 (which he identifies with the caption Pacioli. Dodecahedron net from “Divina Proportione” Venice 1509. Drawing by Leonardo da Vinci^{Footnote 95}) for a later edition of Divina Proportione.^{Footnote 96} This image is no other than a test print from the woodblock in the Albertina Museum shown in Fig. 36. The smaller pentagons inside the larger are the faces of a snub dodecahedron inscribed in the dodecahedron. This test print could not have been known to Pacioli or Leonardo, who, respectively, died in 1517 and 1519, since the woodblocks in the Albertina Museum were carved sometime after 1538.

Dürer was the first to consistently introduce planar nets in Underweysung der Messung, the treatise that he meant, first and foremost, to be instructional and that he wrote, as Peiffer (2004, p. 245) asserts, with “constructive, concrete and material geometry” in mind. Hermann Staigmüller, cited by Friedman (2019, pp. 37–38), notes that Dürer devised solid bodies by studying physical models without necessarily unfolding them and by simply sketching their nets, as Dürer’s notebooks reveal. Remarkable perspective drawings of several solid bodies are found in Dürer’s sketchbooks, yet he does not include any of these in Underweysung der Messung. Instead, he gives the reader the task of crafting models from their nets. Beginning with the tetrahedron, which is shown in plan and elevation and also in a planar net, Dürer (1525, before drawing 29) explains how the latter is to be used, in a sentence that we interpret as follows:

This is how I opened it / after laying it on the ground / and after that, I have raised what was torn open^{Footnote 97}

Dürer adapts this sentence with slight variations for the other regular bodies often referring to the body being shown laid down on the ground (“zugetan nieder in grund gelegt”), torn open (“aufgerissen”), and to the act of raising it or putting it together (“so man die zusamen leget”). As Friedman (2019, p. 34) notes, Dürer never uses the verb to fold or its derivatives and only mentions the act of cutting or tearing apart (“zerschneyden”) when referring to the sphere. Before introducing the “ungeregulirten corporen”, Dürer (1525, after drawing 34) explains:

One can also make many beautiful corpora / that also touch a hollow sphere with their corners, / but have unequal surfaces / I want to draw these in the following / completely open / so that one can put them together with precision. / Whoever wishes to make them neatly, must draw them larger in a double-thick paper^{Footnote 98}/ and cut all the traces with a sharp knife, in one of the sides of the reinforced paper / so that the surfaces may be detached from the remaining paper / and then the whole corpus can be put together / bending where the lines were traced. / Pay attention to what will be explained, / because, from this, one can make many useful things.^{Footnote 99}

Regarding the planar nets in Underweysung der Messung, Friedman (2019, p. 50) discusses the possibility that Dürer might have followed the example of Pacioli and Leonardo and that of the French mathematician and philosopher Charles de Bovelles (1479–1567). Bovelles included planar nets of the Platonic Solids and other bodies in De Geometricis Corporibus. Figure 37 shows the net of a solid body that Boveles (1510, p. 377) describes and our interpretation on the right. If we assume that all the faces are regular, Bovelles conceived the elongated pentagonal bipyramid or Johnson Solid J16, which the mathematician Norman Johnson (1966, p. 86) would describe in 1966. The image on the right illustrates five great semicircles of the sphere that circumscribes the prismatic surface. The apexes of the pyramids, however, do not belong to the same sphere.^{Footnote 100}

Dürer could have known Bovelles’ book because he had access to the personal library of Wilibald Pirckheimer, a prominent humanist to whom he affectionately dedicates his treatise.^{Footnote 101} One reason to believe he did is the net shown in Fig. 38, of an elongated hexagonal bipyramid^{Footnote 102} from Underweysung der Messung, comparable to the one Bovelles had described in 1510. Curiously, in folio 451.r and folio 501.r of the Codex Atlanticus, which Leonardo would have drawn in 1516 and 1517, there are a few sketches of an elongated hexagonal bipyramid similar to the one Dürer drew. This coincidence hints at the possibility that Leonardo and Dürer studied the same solid body or that Dürer, at some point, would have known Leonardo’s drawings or vice-versa. In our interpretation of the elongated hexagonal bipyramid in Fig. 38, we took into account Dürer’s remark that all the vertices should touch a hollow sphere (1525, after drawing 34) and that the triangular faces of the solid body in drawing 43 are isosceles with the same height as the longer edges of the six rectangular faces:

If you put six quadrangles with right angles one after the other / and 12 triangles, each of which is exactly as high as one of the six parts / and then join everything together, you can make a body out of it, that is shown here torn open.^{Footnote 103}

Regardless of the possibility that other authors influenced Dürer, his decision to include polyhedral nets in Underweysung der Messung was groundbreaking. To begin with, because of the level of abstraction involved with independently devising planar nets from models of solid bodies and vice-versa and, even more importantly, because, by doing so, Dürer intended to share with his readers the possibility of experiencing solid geometry in a tangible form that can thus be, in the words of Andrews (2016b, p. 45), “touched, handled, manipulated and experimented with”. Practically a novelty in the literature of his time, this method of graphically describing solid bodies would shape our understanding of mathematical models and all subsequent developments of polyhedral theory. It would also pave the way, as Friedman and Rougetet (2017, p. 7) sustain, to the German mathematical tradition of describing polyhedra with edge unfolding.^{Footnote 104}

Augustin Hirschvogel names the revolutionary method introduced by Dürer as “rete” or “netz” and uses it to graphically describe ten solid bodies in his book, so that his readers can turn each into what Hirschvogel (1543, Part 2 of Chapter 4) identifies as “ein materlich Corpus” or a material Corpus. Thanks to the success of Geometria, Hirschvogel became the author in Early Modern Germany who, following in Dürer’s footsteps, best disseminated this new form of understanding mathematical concepts. In a manuscript version of La Pratica della Perspettiva,^{Footnote 105} Barbaro refers to manipulating physical models of solid bodies as the act of studying the material body in hand, which gives us an interesting insight into his reasoning. Before Hirschvogel and Barbaro, Pacioli (1509) had used the expression “corpi materiali” to describe Chapter LV in the table of contents and spoken about “material forma” in Chapters LII and LIII and “figura material” in Chapter LII of Pars Prima.

Barbaro describes 32 solid bodies with a planar net that he names spiegatura, a term which, according to Monteleone (2019, p. 77), can be interpreted as an unfolding. It is possible that Barbaro chose this term because of its double meaning, as it seems to derive from the verbs spiegare (to explain) and piegare (to fold). Barbaro (1568, p. 45) further explains that a spiegatura consists of an open figure and that a three-dimensional model can be used to explain how the plan views are obtained:

To describe the bodies, we will follow this order, which, in the first place, will present their unfolding and after, their perfect plan, degraded, and finally, correct, their shadowing. By unfolding, I mean the description of the open figure, from which is made the whole body folding it together to demonstrate the true form, a thing that is truly practical and delightful to transform many bodies into lanterns and other uses of pleasure.^{Footnote 106}

In fifteen solid bodies that were probably too complex to describe with plan views or perspective drawings, Barbaro only presents spiegature. The fact that the written description is short in most and only a partial planar net is included, and also that many of these solid bodies were unknown in Barbaro’s time lead us to believe that they never got to be built as three-dimensional models and were only devised as planar nets. In the following, we discuss how planar nets might have been determinant for Albrecht Dürer devising the snub cube and for the Anonymous Author to conceive several complex situations.

3.1 Das Sechste Corpus of Albrecht Dürer

The description of the snub cube by Dürer (and Archimedes long before him) is a remarkable achievement in itself since it is far more complex to obtain than any other Archimedean Solid derived from the cube. After Dürer, the Anonymous Author would describe the planar nets of the cube and the octahedron with a snub cube on the inside (as well as a snub dodecahedron inside the dodecahedron and the icosahedron). We have seen two of these woodblocks in Figs. 18 and 36. In 1619, Kepler would describe the snub cube and the snub dodecahedron in a time when the configuration of the thirteen solid bodies was already known throughout Europe. The snub cube is obtained from the cube by uniformly expanding its faces outwards to a specific distance, and rotating them clockwise or counter-clockwise at an exact angle (or vice-versa, first rotating and then expanding) until the distance between the closest vertices equals the edge length of the squares. The space between the squares is then filled with 32 regular triangular faces. The fact that the snub cube cannot be obtained through a compass and straightedge construction alone^{Footnote 107} hints at the possibility that Dürer could have devised the sixth of his ungeregulirten corporen from a planar net.

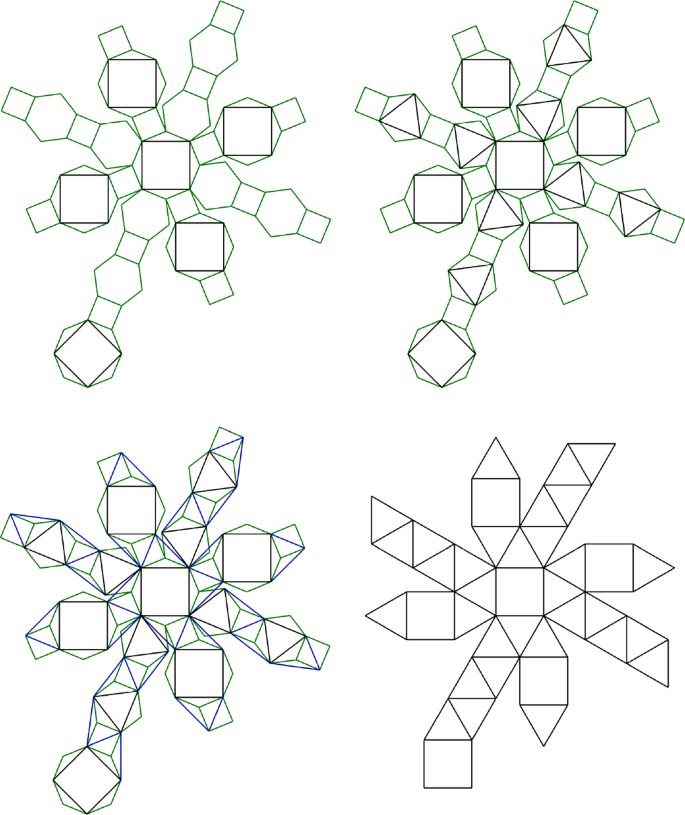
We have concluded in Table 1 that Dürer was the first author to describe the snub cube and the rhombitruncated cuboctahedron. This is somewhat revealing since a non-uniform version of the former is obtainable from the latter through a procedure that, many centuries later, came to be known as alternation.^{Footnote 108} With this operation, a new polyhedron is outlined by picking up alternate vertices from the even-sided faces of another polyhedron. If Dürer devised solid bodies from planar nets, as suggested by Staigmüller, cited by Friedman (2019, pp. 37–38), he might have studied a planar net, or even a model of the rhombitruncated cuboctahedron, and drawn six squares from the octagonal faces and eight equilateral triangles from the hexagonal. Even if the space between them is not filled with regular faces, the fact they are triangular may have given Dürer the idea of trying out another net with the same type and number of faces in which the triangular are equilateral instead of scalene.

We illustrate this procedure in Fig. 39: in the first and second steps, squared and triangular new faces are respectively obtained from alternation of the octagonal and hexagonal faces. In the third step, one diagonal of each square is an edge common to two scalene triangles. The last image is a modification of the previous, in which the scalene triangles are perfected and converted into equilateral. Dürer would have thus obtained a planar net for the snub cube, as the last image shows. Figure 40 simulates the same procedure in three-dimensional space: in the first and second steps, the octagonal and hexagonal faces of the rhombitruncated cuboctahedron are replaced by regular faces, respectively square and triangular; in the third, a diagonal of each square is a common edge to a pair of scalene triangular faces. The last step shows how the snub cube is obtained by changing the 24 irregular faces into regular ones and joining these with the previous squared and triangular faces.

Dürer may have devised the snub cube from the rhombitruncated cuboctahedron, but he described the latter after the former in Underweysung der Messung. In his description of the irregular bodies, Dürer mentions the number of vertices and edges in each solid with regular faces. The sixth body is the last of a set of three with 24 vertices that include squared faces: the truncated octahedron (drawing number 38), the rhombicuboctahedron (drawing number 39), and the snub cube (drawing number 40). Given that the rhombitruncated cuboctahedron is the only solid body with 48 vertices, 72 edges and three different types of faces, its complexity might have been the reason why Dürer placed it as the last of the solid bodies with regular faces, and after the snub cube.

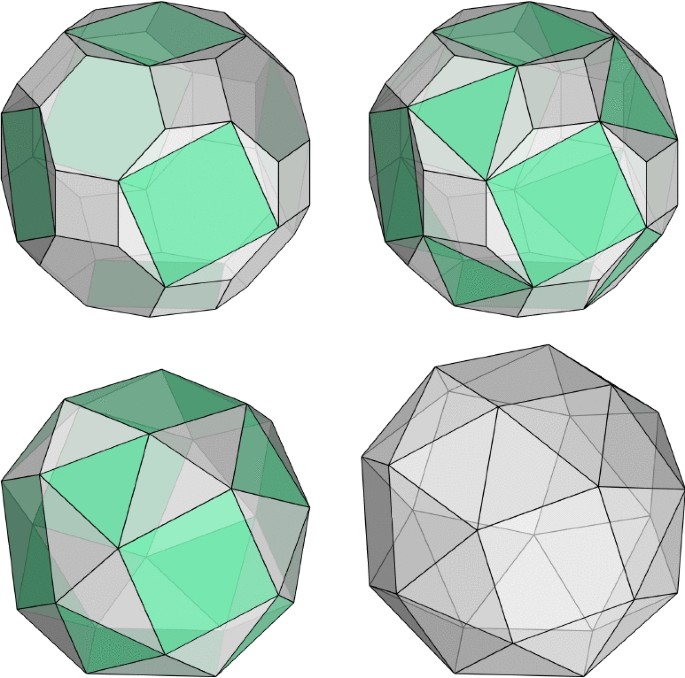
To obtain the rhombitruncated cuboctahedron, Dürer could have divided the edges of the cuboctahedron into three equal parts and drawn the resulting faces either in a planar net, as suggested in Fig. 41 or, directly, in a physical model, as Fig. 42 simulates. He would have thus obtained eight regular hexagons, six irregular octagons, and twelve rectangles, yielding a non-uniform rhombitruncated cuboctahedron (similar to the one Jamnitzer drew in Fig. 24). Dürer would have then changed the resulting net, converting the irregular octagons into regular and the rectangles into squares to obtain the uniform rhombitruncated cuboctahedron. If Dürer ever got to describe the rhombitruncated icosidodecahedron in 1525, we may speculate that he would have also tried out its alternation and obtain the snub dodecahedron.

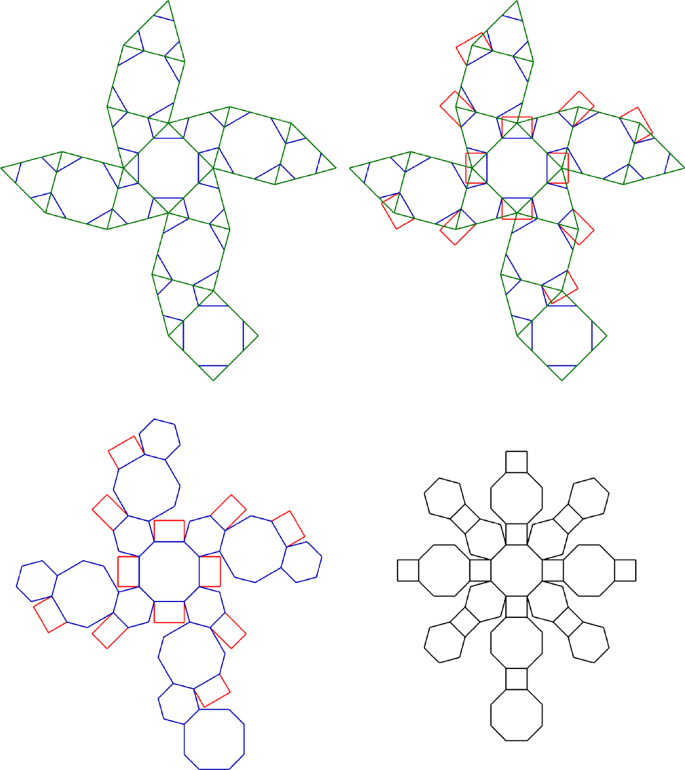
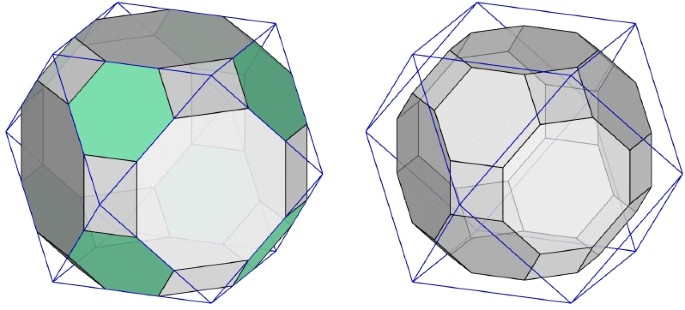
There are two descriptions of the rhombitruncated icosidodecahedron in woodblocks of the Albertina Museum, drawn by the Anonymous Author: in HO2006/703, the decagonal faces of the rhombitruncated icosidodecahedron share the same planes as those of the dodecahedron; in HO2006/711, the hexagonal faces share the same planes as those of the icosahedron. Stöer (1600, folios 120 and 167) drew the rhombitruncated icosidodecahedron in two watercolours but we do not know when they were painted. In La Pratica della Perspettiva, Barbaro (1568, p. 100) described the rhombitruncated icosidodecahedron with a partial spiegatura (Fig. 26).

Returning to the sixth body, it is interesting to note that Barbaro knew Underweysung der Messung well but refrained from including the snub cube in his treatise. This might have been so because, similar to Pacioli, Barbaro was devising solids primarily by truncation and augmentation, not by alternation.^{Footnote 109} A different approach that Dürer would have used to devise the snub cube might explain why it never became a Chapter in La Pratica della Perspettiva: Barbaro only chose to describe the solid bodies he knew how to obtain. As we have seen, Simon Stevin included its planar net in Problematum Geometricorum but said he did not know how to obtain the solid body.

3.2 Solid bodies within the tetrahedron and the octahedron described by the Anonymous Author

An analysis of every planar net from which the Anonymous Author devised solid bodies is beyond the scope of this study, but we will examine a few. The only woodblocks that involve the net of the tetrahedron are shown in Fig. 43. The one on the right is not meant as a net for the truncated tetrahedron since it had been given in Fig. 17. Its purpose is to illustrate how, by dividing the edges of the regular tetrahedron into three equal parts, we obtain the truncated tetrahedron, the same way Piero had explained it in Fig. 5. The unmarked, white hexagonal faces share the same planes as those of the tetrahedron, while the parts to be left out are covered with a dark-hatched pattern. Hence, this woodblock does not offer a solid body but one inside another: a truncated tetrahedron inside the tetrahedron. A different interpretation of the dark patterns would be that they stand for inverted pyramids or dimples. Although Jamnitzer drew solid bodies with comparable concavities (for instance, in 1568, Plate B.I), we do not think the Anonymous Author, in this case, had such concavities in mind.

The woodblock on the left shows another truncated tetrahedron whose triangular faces and those of the tetrahedron are coplanar. The first image in Fig. 44 shows a possible procedure to determine its vertices: by dividing the edges into three equal parts and drawing six cevians, we determine triangles with vertices in the specific intersections mentioned by Gheorghiu and Dragomir (1978, p. 213). The second image shows that the (orthogonal) projections of this truncated tetrahedron do not match the hatched pattern that surrounds the small, white triangles. However, they might have been perceived as such by someone holding a three-dimensional model in their hands. The white triangles are coplanar with the tetrahedron and also with the larger truncated tetrahedron, as the middle row in Fig. 44 shows. We thus have three solid bodies: a small truncated tetrahedron inside the larger and both inside the tetrahedron. Their relations would only be evident to someone who knew the truncated tetrahedron firsthand, as the lesser one never gets to be seen but is only implied.

The penultimate image shows an interpretation of the hatched patterns in Fig. 43 as augmentations, which yields a solution that vaguely resembles certain drawings in Perspectiva Corporum Regularium (for instance, in Plates A.II and A.III) and in Geometria et Perspectiva: Corpora Regulata et Irregulata (watercolour 252). For the protruding triangles to match the planar net, the truncated tetrahedra joined face-to-face with the inner truncated tetrahedron are not uniform. One cannot help but recognize that explaining this solid body from such a planar net and making a model from it is highly impractical. On the other hand, based on the analysis of other situations, the Anonymous Author might have intended to show something else: another solid body laying inside the tetrahedron. The final image in Fig. 44 suggests what the Anonymous Author could have envisaged: a regular octahedron inside the other bodies. The edge length is the same as the small truncated tetrahedron. Our analysis of other planar nets with similar patterns has led us to a significant conclusion: the hatched patterns surrounding the smaller, unmarked faces might not be meant as projections of any face, but rather a representation of the empty space around the smaller body on the inside.

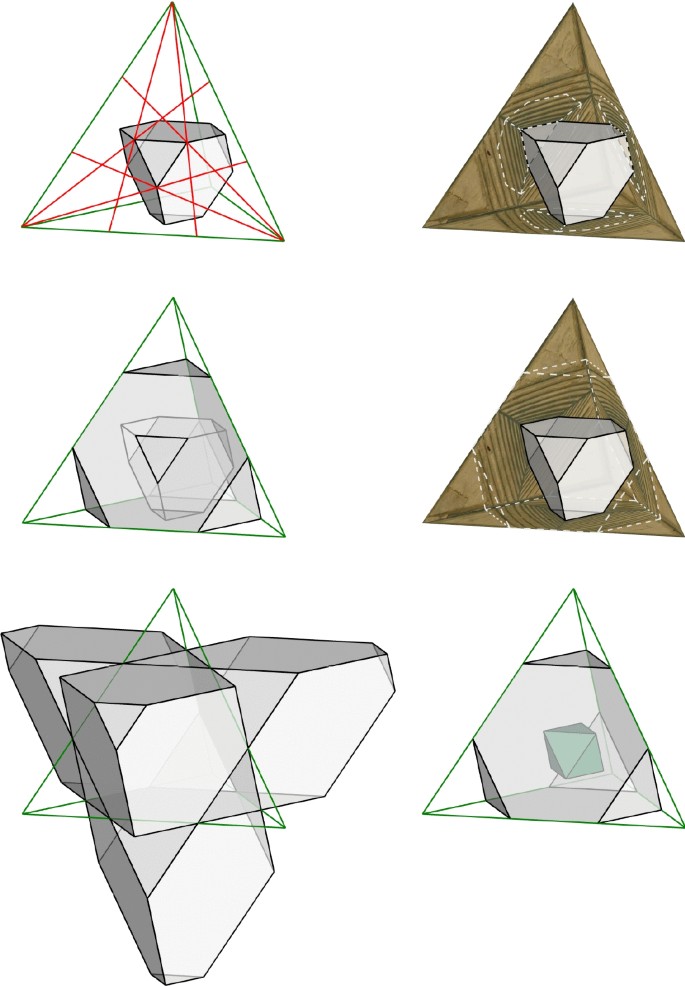
We begin our analysis of the woodblocks involving the octahedron with the simplest case: the truncated octahedron inscribed on the octahedron in Fig. 45 with our interpretation on the right. The vertices of the latter have been truncated after the edges were divided into three equal parts. The resulting unmarked faces and those of the octahedron are coplanar, while the dark-hatched pattern emphasizes how its vertices must be cut off to obtain the truncated body. Figure 46 is meant to show, in the first place, a rhombitruncated cuboctahedron inside the octahedron. On the right is our interpretation of a possible construction the Anonymous Author could have used to determine its vertices: the edges of the octahedron are divided into five equal parts, after which six lines are drawn to obtain a regular hexagon. By replicating the procedure in every face and connecting the closest vertices, we obtain a rhombitruncated cuboctahedron, albeit not uniform, since the edge length of the hexagons is slightly different from other edges.^{Footnote 110}

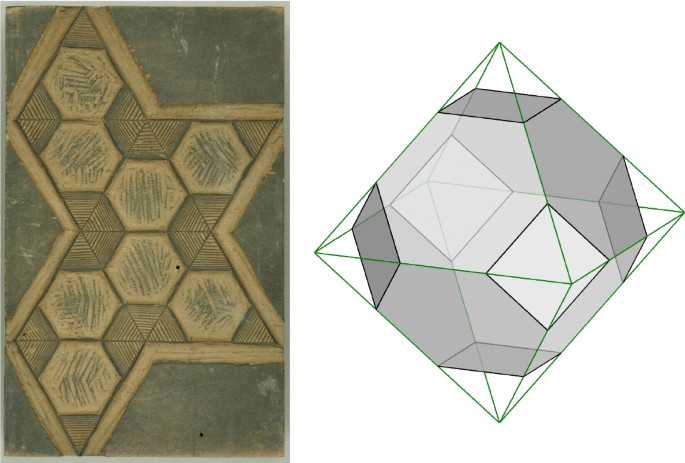
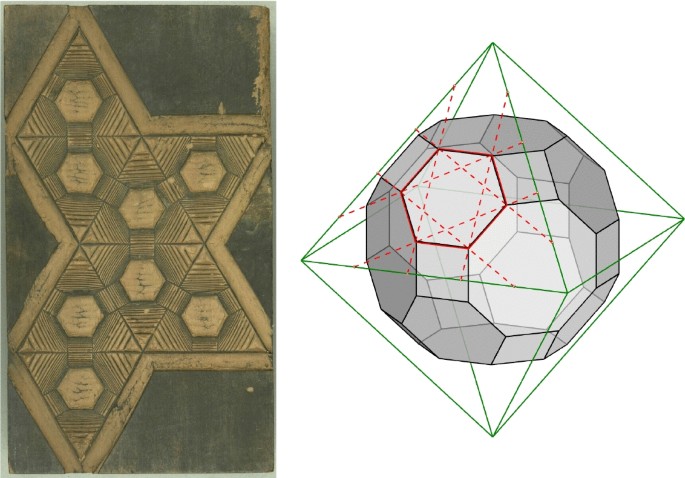
The pattern in the triangular patches that became octagonal faces after the model is folded becomes larger and evolves into small squares around the vertices of the octahedron. The edges are parallel to those of the hexagonal faces. Although this gradient pattern might simply indicate that the resulting octagons and the faces of the octahedron do not share the same plane, the fact that the same pattern occurs in specific planar nets, indicates that the Anonymous Author meant to show other solid bodies besides the most obvious. To understand what the gradient pattern might correspond to, we determined squares approximately the size of those whose edges, in a folded model, are closer to the vertices of the octahedron. The first image in Fig. 47 illustrates a procedure the Anonymous Author could have adopted to obtain the vertices of the small squares, by intersecting the minor diagonals of the octagonal faces.

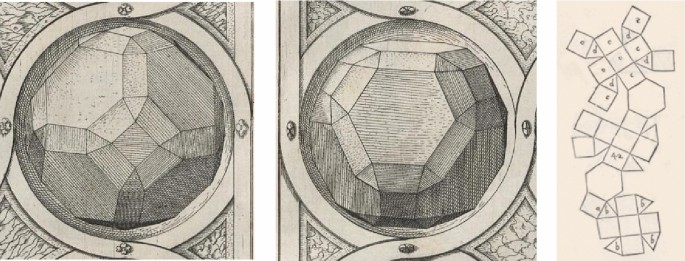
The second image shows that the resulting squares share the same planes as those of the rhombitruncated cuboctahedron, but their convex hull is a non-uniform truncated octahedron. If the Anonymous Author only had regular faces in mind, the squares in the gradient pattern would not have been conceived for this particular truncated octahedron but perhaps for its uniform version shown in the middle row.^{Footnote 111} In the fourth image, there are three prisms connecting the squares in parallel faces which yield the uniform cuboctahedron illustrated in the fifth image. In this case, as well as in the uniform truncated octahedron, the gradient pattern would simply indicate the empty space between the exterior and interior bodies.

The last image in Fig. 47 is another interpretation in which the small squares stand for augmentations of the rhombitruncated cuboctahedron with square cupolas. The gradient pattern suggests the surface between the squares and hexagons of the rhombitruncated cuboctahedron and the protruding squares, rather than the existing edges. Curiously, this interpretation resembles the drawings in Fig. 48 that would be published in 1568. Jamnitzer (1568, Plate B.II) drew the first two in Perspectiva Corporum Regularium although with edge lengths different from ours. The last one is a partial planar net of a concave body with regular faces that Barbaro (1568, p. 103) included in La Pratica della Perspettiva and was identified by Viana (2023b, pp. 122–123) as a rhombitruncated cuboctahedron augmented with square cupolas.

Moving to the woodblock in Fig. 49, our first interpretation of the planar net shows a cuboctahedron enclosed by an octahedron whose vertices were truncated in the edges’ midpoints. Similar to the previous case, the hatched pattern in the square faces evolves into smaller squares, so another solid body seems to be implied. Interpreting the smaller polygons is simpler than before because their configuration is the same as the faces from which they derive. As to the cuboctahedron in Fig. 50, we divided the edges of a squared face into three equal parts in the first image, and drew auxiliary lines to obtain a square roughly the same size as those in the planar net. By conveniently extruding this and other squares, we obtain the smaller cuboctahedron shown in the second and third image. The last image in Fig. 50 shows another interpretation, a concave polyhedron with trapezoidal faces connecting the triangles of the larger cuboctahedron with the squares of the smaller.^{Footnote 112}

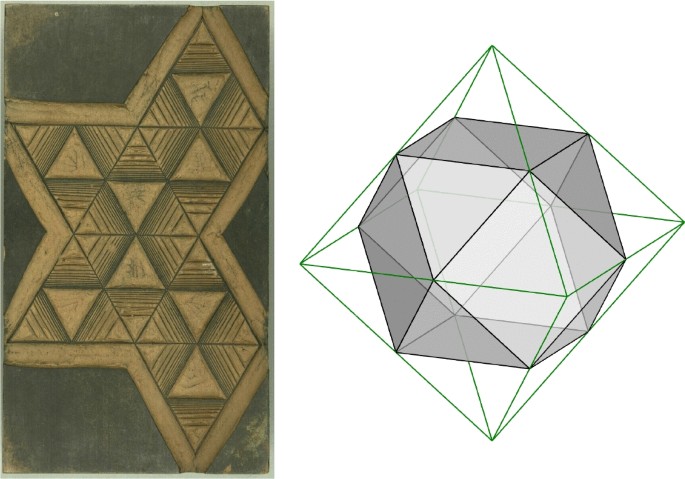
According to our conjecture in a previous section, Dürer could have conceived the snub cube by studying a planar net or a model of the rhombitruncated cuboctahedron. If he lived longer, we have no doubt Dürer would have described the rhombitruncated icosidodecahedron and, subsequently, the snub dodecahedron. But it was up to the Anonymous Author to continue the investigations initiated by Dürer and describe these two solid bodies. In addition, he accurately deduced how every Archimedean Solid (with the obvious exception of the truncated tetrahedron), derives from a pair of Platonic solids. Knowing, at the time, how the cube and the dodecahedron respectively enclose the snub cube and the snub dodecahedron is remarkable in itself. Deducing how these can be respectively inscribed inside the octahedron and the icosahedron would not have been possible without three-dimensional models, and determining their vertices with such precise approximation is absolutely groundbreaking. No contemporary of the Anonymous Author (or even Kepler, who would be born in 1571) achieved such brilliant conclusions. If circumstances had been favourable, the Anonymous Author would have published a book with these and other results, the complexity of which would still surprise us today, undoubtedly setting yet another milestone in the history of polyhedra in the sixteenth century.

Figure 51 shows an interpretation of the planar net the Anonymous Author devised to show how to inscribe the snub cube in the octahedron. The snub cube and the snub dodecahedron are chiral polyhedra, meaning that they lack mirror symmetry and that each exists in two versions, one being the mirror image of the other, as our left and right hands. Their mirror images cannot be superimposed onto another unless the mirror plane is “turned over”, as Cundy and Rollet (1989, p. 63) note. Weissbach and Martini (2002) have demonstrated that, given the diameter of the circumsphere of the snub cube and the snub dodecahedron, the edge length cannot be determined with compass and straightedge alone. Pugh (1976, p. 18) notes that if we divide the edges of the tetrahedron in (1 +

) / 2 (the golden ratio) and define specific cevians, their intersections determine the vertices of the regular icosahedron. The icosahedron can thus be considered a snub tetrahedron, a conclusion to which, according to Pugh (1976, p. 18), Kepler had also arrived. Using a similar procedure in the octahedron and icosahedron, Rotgé obtains the snub cube and the snub dodecahedron.^{Footnote 113} Dividing the edges of an equilateral triangle into specific ratios, Rotgé (1984, 17–19) obtains similar triangles with equal centre of rotation. By applying the procedure to polyhedra with triangular faces, he obtains other polyhedra still.

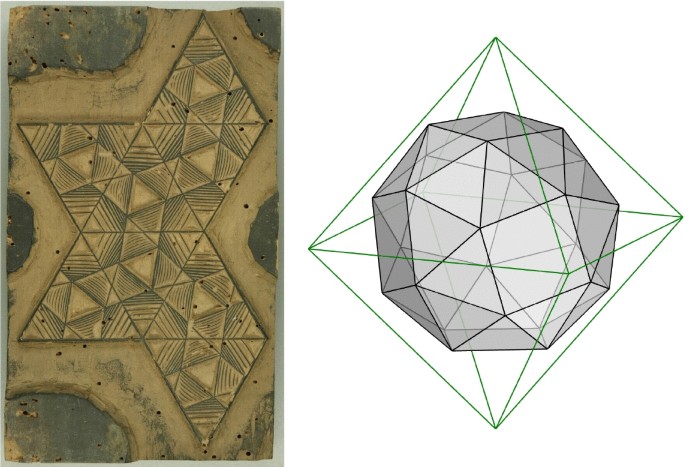
Assuming that the Anonymous Author determined the vertices of solid bodies only with geometric constructions, we illustrate in Fig. 52 a possible procedure to obtain a snub cube, in a fair approximation to the uniform version (Cf. Figures 51 and 52). The vertices are close to their exact location but only specific sets of edges have the same length.^{Footnote 114} The first image in Fig. 52 shows how, by dividing the edges of the octahedron into six equal parts and tracing six cevians, we obtain a triangular face (other attempts we made with a different number of cevians were much less precise). Replicating the procedure in the remaining faces yields the non-uniform snub cube shown in the second image, which has two sets of faces with different edge lengths (six squares and eight equilateral triangles) and 24 scalene triangles. In addition to the snub cube inside the octahedron, the Anonymous Author could have been showing the cuboctahedron laying inside it, as the hatched pattern in the planar net indicates. The last images in Fig. 52 illustrate a possible procedure to determine the small squares in the gradient pattern. The edge length of these squares was determined from the previous division of the edges of the octahedron into six equal parts. By extruding these squares, we determine the square faces of the cuboctahedron shown in the last image.

3.3 Who might the Anonymous Author be?

The information we gathered about the printing woodblocks in the Albertina Museum, as well as the graphic quality and inventiveness of the planar nets, lead us to believe that the Anonymous Author was an artist versed in solid geometry, most likely, from the circle of people working in Nuremberg. Arts and mathematics flourished to an unprecedented level in Early Modern Germany. Jean–Étienne Montucla (1725–1799), cited by Flocon (2006, p. 16), says that nowhere in the world were so many geometers gathered but in Germany in the sixteenth century. Nuremberg was a vibrant cultural city central to Europe, one of the greatest of the Northern Renaissance^{Footnote 115} where several geometers, artists and artisans worked under the enduring influence of Dürer.

Given the woodblocks’ association with Hieronymus Andreae, whoever devised the planar nets was someone who lived in Nuremberg, another city in the German states, or even another country, but with a solid connection to Nuremberg. Furthermore, the Anonymous Author has proven to have a sound knowledge of compass and straight-edge constructions and an evident intention of making complex concepts clear and visually understandable. These nets were undoubtedly part of a larger project which, for some reason, the author could not develop into a published form. Perhaps external funding was impossible, or the author lost interest in the project due to its complexity (or impracticability). He may have also died before being able to continue it. Any author corresponding to such a description had to have shown some prior research about the Archimedean Solids – the more consistent, the better. Further research is necessary, but none of the authors we have studied has shown anything that might suggest the complexity of the Anonymous Author’s studies, which are undoubtedly a development of previous work.

With the death of Hieronymus Andrea, it is safe to assume that his workshop stopped labouring, if not immediately, shortly after 1556. Dürer had died 28 years before and Hirschvogel 3 years earlier, in 1553. Johannes Kepler is excluded from the possibility of being the Anonymous Author, not only because his treatment of the Archimedean Solids is different, but more importantly, because he would only be born 15 years later. The same about Simon Stevin, who was 8 years old by then. The year of birth of Lorenz Stöer is unknown, so we do not know his age in 1556, but he was active at least until 1599, the last date registered in his watercolours. Even so, we do not think Stöer could have been the Anonymous Author: no planar nets are found in his works nor records of the entire set of Archimedean Solids. A few of his watercolours resemble possible interpretations of certain woodblocks, but his studies do not seem as systematic and consistent as the ones we infer from the Anonymous Author. Wade (2012, pp. 208, 222–227) mentions an Anonymous Author who would have lived around 1565 and 1600 and whose watercolours depict exquisite solid bodies, most of which similar to Jamnitzer and Stöer.^{Footnote 116} For reasons similar to Stöer and the author’s young age at the time, nothing suggests that this person could have created the nets in the woodblocks.

Jamnitzer was 49 in 1556, but he did not address planar nets in his book, which would be published 12 years later. Jamnitzer depicted a few solid bodies inside others in Perspectiva Corporum Regularium and mentioned a vague intention of working on a second volume. However, as we have seen, Jamnitzer did not intend his [first] book to be genuinely instructional or, at least, to the extent to which a systematic study such as these nets would comply. Moreover, if he had devised the entire set of Archimedean Solids before 1568, he would undoubtedly have included them in his book. Jamnitzer died 17 years after publishing Perspectiva Corporum Regularium and no records about a second book project have been found. If he conceived planar nets after 1568, Hieronymus Andreae was already dead by then. Furthermore, Perspectiva Corporum Regularium succeeded not only because of its inventiveness but also because of the delicate drawings that Jost Amman had prepared from copper plates, and that many authors would replicate in Jamnitzer’s time and beyond. Returning to woodblock printing would surely mean a retrocess in the quality of his work. For these reasons, we do not believe the Anonymous Author could have been Jamnitzer.

In our search for the Anonymous Author, we compared the nets in Fig. 17 with those that were drawn by Hirschvogel and Barbaro, the only authors who, after Dürer, developed original and systematic studies about the Archimedean Solids in the sixteenth-century and included planar nets in their publications. We have not considered Dürer for the reasons mentioned earlier, and also because, so far, we have not found any studies he had developed which might be comparable to those of the Anonymous Author. The nets drawn by Hirschvogel in Geometria are the same as the ones Dürer drew in Underweysung der Messung, with the exception of the icosidodecahedron. As to the nets in the woodblocks, no indication exists about how each would have to be placed on the page before printing. Therefore, we are not considering the orientation in which the Albertina Museum chose to photograph the woodblocks as an imposition. Two nets are considered the same even if one is rotated when compared to another. Moreover, to compare nets in printing woodblocks with nets printed on paper, we analysed the former in their reflected versions.

Since the planar net drawn by Hirschvogel for the icosidodecahedron differs substantially from Dürer’s (Cf. Figs. 12 and 13), we compared it with the reflected version of the net in Fig. 17, with which the Anonymous Author describes the icosidodecahedron. We also compared the latter with the net of Barbaro in Fig. 25. The three planar nets are shown in Fig. 53. There are evident similarities between the nets on the left and the net on the right. Hirschvogel highlights the rotational symmetry of the icosidodecahedron, and so does the Anonymous Author. The coincidence between the vertical line, the circle and the vertex of the upmost pentagon is not exact but very close. Both nets were developed according to the same principle, the difference being the disposition of the third row of pentagons and subsequent layers. The net that Barbaro included in La Pratica della Perspettiva, on the other hand, is precisely the same as the Anonymous Author.

For the sake of completion, we compared the nets of the Platonic Solids drawn by Hirschvogel, the Anonymous Author, and Barbaro (excluding the cube). The nets that Hirschvogel drew for the tetrahedron, octahedron and icosahedron, shown in Fig. 54, are the same as Dürer. The woodblocks for the octahedron, dodecahedron, tetrahedron, and icosahedron, shown in Fig. 55, are different from any other we have seen until 1568. Figure 56 shows the planar nets of the octahedron, dodecahedron and icosahedron that Barbaro included in manuscript It. IV, 39 (= 5446), which belongs to Biblioteca Naziolane Marciana in Venice. The perfect that Barbaro (1568, p. 45) includes in La Pratica della Perspettiva is similar to the woodblock with the net of the tetrahedron. It is also the same as the net Bombelli (1929, p. 279) includes in manuscript B 1569 of the Archiginnasio Library in Bologna; and that of Stevin (1583, p. 68) in Problematum Geometricorum. Since only two possible nets exist for the tetrahedron, this coincidence does not imply any relation between the authors.

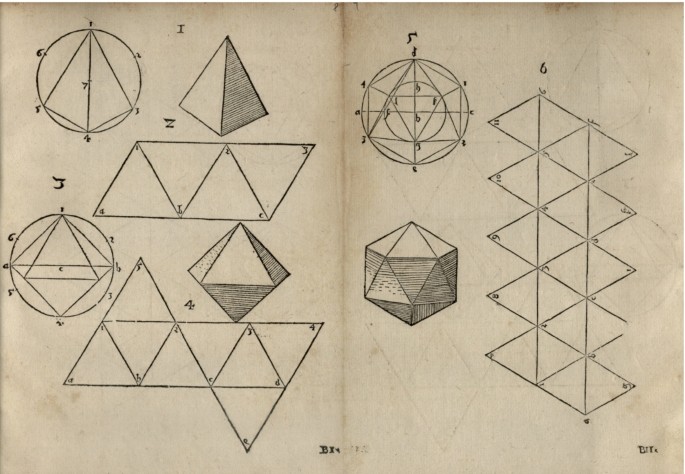
The net of the dodecahedron that Barbaro includes in the manuscript is the reflected version of the woodblock in Fig. 55. The net of the octahedron, which is very distinctive, is also the same in both authors. Comparing the net of the icosahedron by the Anonymous Author and the net in Barbaro’s Manuscript It. IV, 39 (= 5446), the difference resides in the placement of a few faces. The Anonymous Author has two linear sequences of eight triangles and one linear sequence of nine (here, faces that belong to different sequences are counted more than once). Barbaro has three linear sequences of seven triangles (likewise, some faces are counted more than once). Apart from this detail, they are fundamentally the same and yield the icosahedron. Barbaro has nine planar nets in common with the Anonymous Author.

The following summarizes our comparison between the nets of the Platonic and Archimedean Solids of the Anonymous Author with those by Dürer in Underweysung der Messung, Hirschvogel in Geometria, and Barbaro in La Pratica della Perspettiva and manuscript It. IV, 39 (= 5446):

• The tetrahedron is similar to the perfect in La Pratica della Perspettiva;
• The cube is the same as all the authors;
• The octahedron is the same as La Pratica della Perspettiva and manuscript It. IV, 39 (= 5446);
• The dodecahedron is the same as La Pratica della Perspettiva and manuscript It. IV, 39 (= 5446);
• The icosahedron is the same as in Manuscript It. IV, 39 (= 5446);
• The cuboctahedron is the same as all the authors (minus the extra triangular face in Barbaro’s net);
• The icosidodecahedron is similar to the one in Geometria and equal to La Pratica della Perspettiva;
• The truncated tetrahedron is the same as in La Pratica della Perspettiva;
• The truncated octahedron is the same as in Underweysung der Messung and Geometria;
• The truncated dodecahedron is original;
• The truncated icosahedron is original;
• The rhombicuboctahedron is similar to the one in La Pratica della Perspettiva;
• The rhombicosidodecahedron is original;
• The snub cube is the same as in Underweysung der Messung;
• The snub dodecahedron is original.

Barbaro would have been 42 when Andreae died, but we have not found records of Barbaro visits to the German States or any reference to him sending his work for printing in Nuremberg. We do not believe the Anonymous Author could have been Barbaro because his treatise does not include any systematic research on Archimedean Solids inside the Platonic (other than the truncated cube and the rhombicuboctahedron inside the cube). Besides, Barbaro did not include the snub cube and the snub dodecahedron in his treatise. It was not unusual at the time for authors to take inspiration from others without crediting their sources, and Barbaro taking inspiration from the works of Piero della Francesca, Albrecht Dürer, Sebastiano Serlio and other authors has been documented.^{Footnote 117} Since the woodblocks were never used for other than test prints, Barbaro may, at some point, have had access to the nets in a manuscript version or test prints. Perhaps the Anonymous Author shared his ideas with Barbaro, whether by visiting him in Italy or exchanging correspondence. Italy and Germany have always had a special relationship.^{Footnote 118} As early as the thirteenth century, the Republic of Venice had welcomed Germans in Fondaco dei Tedeschi (2023) including merchants from Nuremberg, Judenburg and Augsburg, who stored their goods in the palace. Our Anonymous Author was probably not a merchant, but he might have visited Venice and met Barbaro. We are inclined to believe that Barbaro drew inspiration from the Anonymous Author, but the possibility that both authors independently described the same planar nets should not be excluded.

Comparing the nets of the Anonymous Author with those by Bombelli (1929, pp. 279, 285, 294), we conclude that the tetrahedron is identical, as well as the octahedron and truncated tetrahedron we have shown in Fig. 33. Still, we do not think Bombelli could have been the Anonymous Author because he described only three Archimedean Solids. Moreover, the approach of Bombelli to solid geometry, from what the comparison of the nets and his writings allow us to comprehend, differs significantly from the Anonymous Author. It is more the perspective of a mathematician than that of an artist. On the other hand, Bombelli might have known these nets from Barbaro.

After analyzing these and other authors, the strongest hypothesis about the Anonymous Author’s identity remains that of Augustin Hirschvogel, who authored and illustrated the book Geometria. Not much is known about Hirschvogel, who was born in Nuremberg and left the city in 1536 to work abroad. He returned to Nuremberg in 1543 when his book was published, but moved to Vienna the year after, where he was appointed as the city cartographer and came to settle until his death in 1553. Hirschvogel, we recall, was the first to describe the rhombicosidodecahedron after Archimedes. Given his knowledge of the subject and the graphic quality of his work, Hirschvogel may have wished to continue combining his expertise in geometry and planar nets with the description of the irregular bodies he had introduced in 1543. The planar nets in his book would have been adequate developments for someone who had begun studying Underweysung der Messung and planned to expand his studies to another level. The net the Anonymous Author drew for the icosidodecahedron on the upper right in Fig. 53 may be seen as a different version of the one on the left that Hirschvogel drew in 1543. A short note at the end of the second part of Geometria indicates that Hirschvogel (1543, Beschluß des zweiten Teils) did intend to develop his research further and, better still, that his findings would soon be printed:

I still have a lot of related beautiful Corpora / but / not all of them are made / So God willing / these will soon come into print / along with other beautiful hidden pieces.^{Footnote 119}

Pfaff (1996, p. 43) interprets Hirschvogel’s sentence as referring to two of his monogrammed etchings from 1549. However, it is entirely possible that Hirschvogel meant to suggest the existence of more drawings of solid bodies, such as planar nets, that he could not include in his book. The fact that Hirschvogel mentions hidden pieces to be shown within other bodies, hints at the possibility that our interpretation of the planar nets depicting a third solid body inside two others is valid.

The “Nürnberger Künstlerlexikon”, edited by Manfred Grieb (2007, pp. 665–666), tells us that, after moving to Vienna, Hirschvogel remained so attached to his hometown that he sent his maps to Hans Weigel the Elder to be printed in Nuremberg. If Hirschvogel had plans for a book project, he may have sent his preliminary studies to be printed in Nuremberg. The workshop of Hieronymus Andreae, who had twice published Dürer’s treatise, would have been a good choice. The important position Hirschvogel held in Vienna from 1544 onwards may have prevented him from continuing his studies on solid geometry, so a successor for Geometria was never published. The timeline complies with the activities of the printing workshop of Hieronymus Andreae, which would have ceased around 1556. Hirschvogel would have sent his work for printing between 1543, when Geometria was published, and before 1553 the year in which he died. With Hirschvogel’s passing, few people (if any) would have the knowledge and skills necessary to continue his work, so the woodblocks were never used for extensive printing and were eventually forgotten. Although our hypothesis is still a conjecture, we hope to confirm it soon or that information about another artist or mathematician that we may identify as the Anonymous Author is found.

3.4 Conclusions

After a discussion about the historical and cultural context that motivated the fascination with solid bodies of so many artists and mathematicians in the fifteenth and sixteenth centuries, we analyzed the studies developed at the time that revealed to be more consistent on the Archimedean Solids and discussed their contribution to the early history of polyhedra. Such studies were authored by Piero della Francesca, Luca Pacioli and Leonardo da Vinci, Albrecht Dürer, Augustin Hirschvogel, an unidentified Author whose remarkable accomplishments were never published, Wentzel Jamnitzer, Daniele Barbaro, Lorenz Stöer, Rafael Bombelli and Simon Stevin. A chronological summary of this detailed analysis allowed us to trace which authors first described each Archimedean Solid after Archimedes and understand how the authors would have devised the solid bodies that were not found in preceding works.

Understanding how Albrecht Dürer, Augustin Hirschvogel and Daniele Barbaro explored three-dimensional models and polyhedral nets to conceive new solid bodies was a fundamental point of departure for the second part of our research in which we present a conjecture on how Albrecht Dürer could have conceived the snub cube. In addition, we discussed and interpreted six woodblocks with polyhedral nets from the Albertina Museum in Vienna. These extraordinary woodblocks are a materialization of an advanced and unprecedented research on the Archimedean Solids from an unknown author who was active decades before Kepler. We also analyzed the impact of these remarkable studies on other authors who delved into solid geometry in the sixteenth century and pondered the possibility that the Anonymous Author might have been Augustin Hirschvogel. Further research is crucial to substantiate our initial hypothesis or point to another artist with strong connections to the city of Nuremberg as a potential author.

Notes

1. Here, we are paraphrasing Joseph Malkevitch (2013, p. 57), who identifies “Renaissance artists, architects, artisans, and scholars “discover” and “rediscover” various Platonic and Archimedean solids, star-polyhedra, compounds, and other polyhedral objects” as Milestone 9 (out of 23) in the history of polyhedra.
2. According to Kemp (1992, p. 76), the translations and commentaries about the Elements and the Optics by all the major theorists of geometrical perspective in Italy after 1550 were not only crucial to better understand the classical texts but played a critical role in the foundation of perspective science in general and in the studies of three-dimensional geometry in particular.
3. Tormey and Tormey (1982, p. 138) state that, among the several works by Plato that were translated into Latin, the Timaeus was the one who strengthened the prevailing theory on “an isomorphic relation between the mathematical foundation of pictorial representation and the mathematical structure of reality.”
4. Scriba et al. (2015, p. 82) denote that the work by Hypsicles of Alexandria on the regular bodies had been attached to Euclid’s Elements as Book XIV. The author of Book XV, however, add Scriba et al. (2015, p. 100), remains a mystery. The book consists of three parts: the first explains how to generate the Platonic solids by inscribing them in each other; the second discusses the ratios between the edges, and the third explains how to determine the angle between adjacent faces.
5. This paragraph synthesizes the entry about the history of printing in Encyclopedia Britannica (Lechêne, 2020) and Printing and Publishing in the Renaissance by David Wade (2012, pp. 45–46).
6. According to Andersen (2009, p. 375), the objects preferred in perspective drawing treatises were “polygons, circles, some polyhedra (not least the regular polyhedra), crosses, columns, arches, vaults, and simple rooms with a few windows”. Andrews (2016b, p. 16) further denotes that “polyhedral models, most often made from paper or wood (…), were used both as pedagogical aids for learning to understand Euclid and as tools for learning how to draw (themselves) in perspective”.
7. According to Centofanti (2016, p. 148), Le Due Regole was fundamental to perspective science regarding the transition from an artistic experimental approach to a rigorous scientific approach.
8. More about the intarsias in Italy and Germany in Thomas and Williams (2000); Tormey and Tormey (1982); Huylebrouck (2015); and Andrews (2022, pp. 171–185).
9. The mistake in the drawing of the truncated icosahedron, identified by Huylebrouck (2015), is not found in the printed version of Divina Proportione but in the Milanese manuscript. Huylebrouck (2015, p. 463) suggests that Leonardo might not have been the author of the error but the copyists who were responsible for editing the manuscript.
10. Convex regular polyhedra are commonly known as the Platonic Solids, although Plato was not the first to describe them, but Theaetetus of Athens (c.417–369 BCE), according to a scholium in Book XIII of the Elements, which is mentioned by Taylor (1997, pp. 255–256).
11. See Coxeter, Longuet–Higgins, and Miller (1954, p. 402), and Grünbaum (2009), who discusses a local and a global criterion to distinguish between Archimedean and semiregular polyhedra.
12. Coxeter (1973, p. 18) establishes that a quasiregular polyhedron has regular faces, while its vertex figures, though not regular, are cyclic and equiangular. Consequently, all the edges, vertex figures and dihedral angles are equal. The faces are of two kinds, and each face of one kind is entirely surrounded by faces of the other. There are only two convex quasiregular polyhedra.
13. Kepler (1619, p. 61): “Perfectae in solido congruentiae gradus inferioris, species sunt tredecim; ex quibus tredecim oriuntur Archimedêa Corpora.”The translation of this and other sentences from Latin in this study were accomplished with the help of Célia Mafalda Oliveira, to whom we express our sincere gratitude.
14. Unguru (1974) reveals that Vitello Thuringopolonis (c.1230–1280/1314), a Polish friar and natural philosopher whose writings on perspective were extensively used until the seventeenth century, knew at least parts of the Synagoge. As Unguru notes, Propositions 22, 38, and 39 in the book Perspectiva, which Vitello wrote, are identical to Propositions 43, 42, and 44 in the Synagoge by Pappus. Since Vitello did not know Greek, Unguru (1974, p. 312) believes he may have adapted these from a Latin translation or other unknown source.
15. One of the goals of this essay has been to complement essential studies on the subject authored by Judith Field and Kim Williams. Similar to Field (1997, p. 244), we consider the six Archimedean Solids described by Piero, the six described by Pacioli / Leonardo, the seven described by Dürer in 1525, and the eleven by Barbaro. Similar to Williams (2021, pp. 51–52), we consider the six described by Pacioli / Leonardo, the seven described by Dürer in 1525, and the cuboctahedron, icosidodecahedron, truncated tetrahedron, truncated octahedron, truncated cube and rhombicuboctahedron described by Hirschvogel.
16. Kemp (1992, p. 55) refers to Underweysung der Messung as the collection of “fruits of mathematical endeavours” that Dürer had been gathering at least since 1508. According to Peiffer (2000, p. 373), Dürer had bought the translation of the Elements by Bartolomeo Zamberti in 1507.
17. Kemp (1992, p. 62) identifies Hirschvogel, Stöer, Jamnitzer and Lencker as the “Nuremberg Perspectivists”. In addition to these, Peiffer (2000, p. 111) refers to Lautensack and Pfinzing and Andrews (2022, p. 120) mentions Halt.
18. Wood (2003, p. 237) notes that the German perspective books published in the second half of the sixteenth century meant to highlight the appeal of perspective drawing with illustrations of “ideal constructions of fantastic, three-dimensional objects.” Such publications “were finer than the earlier handbooks, but they did not necessarily teach the method of perspective, nor did they make any contributions to the theory of perspective.”
19. According to Banker (2005, p. 168), “That Piero was fascinated by Greek science is demonstrated by his transcription of the Archimedes manuscript, by the three works on the subject that he wrote, and by his apparent frequent consultations of the works of Archimedes and Euclid”. Piero consulted the original texts for long periods, having cited theorems in the Libellus giving precise references to propositions and books.
20. Andersen (2009, p. 35) notes that Trattato d’Abaco complies with the tradition of similar books that deal primarily with arithmetic, some algebra and practical geometry. In the opinion of Andersen, Piero discussed many advanced geometrical objects as polyhedra in Trattato d’Abaco and the Libellus, but his treatment of mathematics stands on an elementary level.
21. Our interpretation of the words by Piero della Francesca is based on the translation by Luca Pacioli (1509, folio 9r, Tractatus Secundus). Likewise, the following references to the words by Piero are based upon the (unaccredited) translation into Italian of the Libellus, which Luca Pacioli incorporated in the Divina Proportione as Primus Tractatus (1509, folios 1–8) Secundus Tractatus (1509, folios 9–15) and Tertius Tractatus (1509, folios 15–27).
22. According to Stover (2023), the “Rule of Three” is an historically used educational tool that verbalizes the process of solving basic linear equations with four terms where only three are known.
23. In the words of Piero (translated by Pacioli (1509, folio 9r Tertius Tractatus)): “Il quatro base triangulare equilatero cheil suo axis e 4. Del diametro d’la spera che il contene se vole cercare. Sappi che dogni quatro base triangulare equilatero e quella proportione da laxis al suo lato che dallato aldiametro de la spera che contene tale quatro base et laxis del quatro base e al diametro dela spera cheil contene como e 2 ad 3.”
24. According to Scolari (2015, p. 229), Pomponius Gauricus (1480–1528/30) explained how to draw a parallelepiped rectangle (representing a book) in parallel mode in De Sculptura, which he wrote in 1504. Scolari adds that the “paralleli modo”, which was widespread during the fifteenth century, is “the thread that binds Piero, Pacioli, Leonardo, and Gauricus, and also runs through Cesariano’s extraordinary 1521 edition of Vitruvius.”
25. Among other authors, Cromwell (1997, pp. 122–126), Williams (2002), Ciocci (2017, pp. 91–108), and Andersen (2009, pp. 35–36).
26. Pacioli (1509, folio 16v, Pars Prima): “Non me pare Excelso Duca in dicti corpi piu extenderme conciosia chel lor processo tenda in infinito per la continua e sucessiva abscisione de mano in mano de li suoi angoli solidi e secondo quella lor varie forme se vengano multiplicare”.
27. According to Field (1997, pp. 253–254), the illustrations in Divina Proportione that were not drawn by Leonardo are “clumsy and in a uniformly old-fashioned (non-perspectival) style, so it seems possible that Pacioli gave his printer a copy of the original vernacular text of Piero’s work (now lost), with Piero’s own illustrations (or copies based on them)”.
28. References about Pacioli using such models are discussed, for instance, by Scolari (2015, p. 219), Peiffer (2000, p. 87) and Ciocci (2017, p. 96).
29. The passage in the words of Pacioli (1509, folio 22r, Tertius Tractatus) is more interesting than our adaptation: “Lectore non te maraviliare se de simili corpi composti de diverse e varie base non te se mette sempre in margine loro figure conciosia ch’le sieno difficilime farle in desegno pero che bisogna che sieno facte per mano de bono perspectivo quali non si posano sempre havere a sua posta si cóme per sua humanita feci el nostro Lionardo da vinci siando a Milano ali medesuni stipendii de lo excellentissimo Signor Duca di quello Ludovico Maria Sforça. Ma quando in questo de sopra e ancora sequente se sieno posti casi alcuni overo che sabino a ponere, basta che tu fra li ante posti dinançe in principio in perspectiva de sua mano recorra peroche da quelli comme a suo luogo denançe fo dicto al capitulo. LV. lor forme procedano in infinito e se ben guardi fra quelli non fo formato el corpo de decagoni pur in questo labiam messo al terço tractato per terço caso e tu deglialtri potrai el simile fare.”
30. Folio 735 is traced back to the year 1495 on the Codex Atlanticus website (1495).
31. Chapter XXIV of La Pratica della Perspettiva by Daniele Barbaro was identified by Viana (2023b, pp. 122–125) as a rhombitruncated icosidodecahedron augmented with pentagonal cupolas.
32. Translating a German treatise into Latin was a significant risk for Camerarius, as discussed by Peiffer (2002, p. 639), but the outcome was a success and the expertise Dürer had developed on practical geometry became accessible not only in other countries but to scholars and academics, whom Dürer did not intend to reach in the first place. According to Peiffer, Dürer may have assisted Camerarius in this translation, which can be considered the first interpretation of this treatise. Camerarius entitled its translation as Alberti Dvreri Fourth Book of Geometric Instructions: Published again, preserving the order of the figures, as the author himself expressed them, in a free translation from “Alberti Dvreri Institvtionvm Geometricarvm Libri Qvatvor: Nunc iterató editi, servato ordine e figuris, sicut ab ipso authore expressae suerunt” (1532).
33. The words Durera (1532) wrote before drawing 29 were: “die der Euclides corpora regularia nennet”.Since the treatise does not include page numbers, for each citation, we indicate the number of the nearest drawing. Every citation from Underweysung der Messung in this study is from Book IV, which deals with solid geometry and perspective drawing concepts.
34. Andrews (2016a, p. 411) says Dürer had a “long-standing access to Euclidean geometry that predated his engagement with Italian perspective” and that he could have met Pacioli, who, by the time Dürer was in Bologna, “would have been working on his own annotated edition of Euclid.”
35. The chronology compiled by Peiffer (2000, pp. 373–374) states that, while he visited Venice in 1507, Dürer bought a copy of the translation of the Elements by Zamberti. In January 1523, Dürer bought ten books from the Regiomontanus–Walter library, where the translation by Campanus of the Elements was found. According to Andrews (2016a, p. 411), although he owned at least two editions of the Elements by 1523, “Dürer evidently maintained a lifelong fascination with Euclid and remained interested in the most up-to-date translations”.
36. Describing the many fields of craftsmanship in which Hirschvogel worked, Andersen (2009, p. 217) explains that, upon understanding how important was the knowledge of geometry, Hirschvogel decided to publish his own “introduction to the discipline” in 1543.
37. Andrews (2022, p. 114) translates its full title “Ein aigentliche vnd grundtliche anweysung, in die Geometria, sonderlich aber, wie alle Regulierte, vnd Vnregulierte Corpora, in den grundt gelegt, vnd in das Perspecktiff gebracht, auch mit jren Linien auffzogen sollen werden”, into An authentic, thorough instruction in geometry, especially how all the regular and irregular bodies are to be inscribed in the ground, and brought into perspective, also illustrated with their lines.
38. Our translation of the words by Hirschvogel “Das Buch Geometria ist mein Namen / All freye Kunst avs mir zvm ersten kamen / Ich bring Architectra und Perspectiva zusamen” combines the translations of Andersen (2009, p. 220) and Andrews (2022, p. 116).
39. Figures 13 and 14 belong to a copy in the Bayerische Staatsbibliothek in München that binds two volumes in one book with the written part first and the drawings second. Another copy at the Staats und Stadtbibliothek in Augsburg has the drawings before the written part. The book in Bayerische Staatsbibliothek has the graphic descriptions alone, some with different shadowing; the pair of plan-views of the rhombicosidodecahedron in a reflected version; and different page numbers.
40. Schmitt (1982) presents further biographic details about Hanns Sebald Lautensack.
41. Schreiber et al. (2008, p. 459) state that “The wooden blocks were seemingly never used for printing a book. The state of the blocks shows that only a few proof sheets were made, and afterwards, minor corrections were made to some of the blocks. Hence, it is not surprising that these woodcuts never were seen on paper.”
42. We are grateful to Dr. Christof Metzger, Curator of the Albertina Museum, for sharing information about this and other publications that mention the printing woodblocks.
43. The title is a translation from “Jahrbuch der kunsthistorischen Sammlungen des allerhöchsten Kaiserhauses”, whereas the reference to the woodblocks has been translated from “holzstockemit geometrischen figuren auf rund der schriftder umschlage nicht spatee als letes viertel des xvi jarhunderts”, which is listed under the Appendix “Plattenbestände in einigen öffentlichen und privaten Sammlunge.”
44. According to Ciocci (2021, p. 138), a preliminary draft was concluded from 1568 to 1569.
45. The website of the Albertina Museum shares details about this woodblock in HO2006/704.
46. Ippolito and Bartolomei (2016, pp. 85–86) note that Tartaglia introduced, in his study of the Solids in each other, a description on how to inscribe “the icosahedron into the cube and the octahedron into the icosahedron.”
47. Axworthy (2021, p. 100) tells us that Foix-Candale published in 1566 “a Latin edition and commentary of the fifteen books of Euclid’s Elements (that is, including the apocryphal Books XIV and XV), to which he added a sixteenth book on the regular polyhedra, as well as a short treatise on mixed and composed regular solids. (…) Foix-Candale’s commentary was reprinted in 1578. He added at this occasion a seventeenth and an eighteenth book, where he pursued his investigation of the properties and relations of the regular polyhedra.”
48. Occasionally, the vertices do not coincide with our virtual 3D models, which is perfectly understandable as the carvings were made in woodblocks, with all the technical predicaments that such a technique implies. Moreover, we cannot evaluate these accomplishments by our modern standards, so the drawings need not be absolutely precise to be accepted as legitimate. If the vertices of an enclosed body are just a short distance from their location in our virtual environment, we assume it to be a regular-faced polyhedron.
49. Gessner, Hashagen, Peiffer, and Tournès (2018, p. 3486) note that Jamnitzer’s perspective machine became widely known thanks to this woodcut, being later copied and adapted by others.
50. Flocon (2006, p. 32) tells us that no documents exist about the circumstances of the collaboration between Amman and Jamnitzer. When he approached him, Jamnitzer was already an important figure in the city, and Amman was 31 years younger. By comparing the etchings done by Amman with the drawings by Jamnitzer in Berlin, Flocon notes that the etchings were as truthful as possible despite subtle modifications and misinterpretations.
51. The labelling of the Plates is unclear to us because the subtitle page presenting the tetrahedron is Plate A.I, while those introducing the octahedron, cube, icosahedron and dodecahedron are A.VI, B.V, C.IV and D.III, respectively. Plate C1, for instance, is the second regarding the cube after the corresponding subtitle page; Plate D.I is the third Plate of the icosahedron; while E.I is the fourth of the dodecahedron. Label E continues in the second part of the book, but F.I is the label on the fifth Plate, which introduces the cube’s variations. The Plates on the sphere, the cone and the torus are labelled G, H and I, respectively.
52. In Fig. 23, the signature “J. A.” is in the very middle at the bottom of the print.
53. Jamnitzer (1568, Plate A.VI): “AER. Der Luftt. / OCTAEDRON / Solidum octo basium triangularium, / Ein Diamant Punct / oder Corper von acht Trianglichten Flechen / Das ander Corpus wirt von acht gleichseitigen Triangeln zusammen gesekt / hat Zwölff senten ecth vierundzwainzig flacher winctel / welche sechs Cörperlicher ecth machen / aus dises Cörpers grundt / durch abschnendung unnd hinnan sezung nach eines neden gefallen / Werden hernach 23. andere unterschidliche Corpora formiret / unnd Fürgerissen.”
54. Jamnitzer (1568, Prologue, third page): “Bit demnach freundlicher lieber lefer / du wolft solchen meinen flenk getrew herziger guter mainung aufnemen / und da ich die danctbartent spürn / werde ich geursacht / den andern thanl berürtfwerts / auch hinaus fomen zulassen. Dañ ob ich wol gewilt gewesen / das ganze werth mit einander getrewlich an tag zubringen / und tructhen zulassen / so hat es doch anderer meiner obligender geschefft / und arbeit halber dissmals nit alles zuglench disponirt und ins kupffer zusammen geordnet werden mugen / es soll aber doch / der bemelt ander theil / durch mittel gottlicher gnad aufs furderlichst auch dem gemainé nuk zu gur ans liecht gelangen.”
55. The edition of Perspectiva Corporum Regularium published by Siruela, prefaced by Albert Flocon and translated by Helena del Amo includes an Appendix entitled Perspectiva Sintagma (2006, pp. 135–138) that explains how to determine the perspective of an equilateral triangle. We have not considered such an addendum in this study because, as the translator states in a footnote (2006, p. 138), the text is thought to be a supplement to a later edition of the book, which Jamnitzer may not have written. It was published in Amsterdam in 1626, 41 years after Jamnitzer’s death.
56. According to Vagnetti, cited by Monteleone (2019, p. 67). Monteleone further notes that Barbaro’s rush to publish the book may have been related “to health problems, as he died about a year later” or maybe for his awareness “that Egnazio Danti was working on Jacopo Barozzi da Vignola’s Le due regole della prospettiva pratica (…) and Francesco Melzi was re-arranging Leonardo da Vinci’s Notes on Painting.”
57. Monteleone (2019, p. 73) notes that “There is unquestionable evidence for stating that Barbaro knew Piero’s work on perspective but, maybe, he might not have known it was by Piero: comparing text and images by Barbaro with the pages of De prospectiva pingendi, one notes many similarities and, in some cases, even precise matches or overlapping details.”
58. According to Field (1997, p. 270), Barbaro’s comment that Piero wrote for “gli idioti” might have been meant as a criticism of the “repetitious drawing instructions which form the bulk of the text in most of Piero’s propositions.”
59. Barbaro (1568, p. 3): “Se forse non uogliamo chiamare precetti, e regole, alcune pratiche leggieri poste senza ordine, e fondamento, e esplicate rozzamente: perche di queste ne sono pure alcune di Pietro dal Borgo S. Stefano, e d’altri, che per gli idioti ci potriano servire. Poche cose ci ha lasciato Alberto Durero, benche ingeniose, e sottili.”Other translations of the word “sottile”, based on the Dizionario dei Sinonimi e dei Contrari of Corriere della Sera (2021) would be subtle, penetrating, intricate, astute, precise, meticulous, skillful, insightful.
60. The nine non-uniform polyhedra in La Pratica della Perspettiva have been identified by Viana (2023b, 2023a).
61. In the edition we analysed, only Chapters II-VI have shadowing but Williams and Monteleone (2021, pp. 206, 201) reveal that other versions include shadowing in the truncated tetrahedron and the cuboctahedron.
62. Having analysed the plan and elevation constructions of the pentagonal dodecahedron by Barbaro, Andersen (2009, pp. 156–158) concludes that, although several procedures that Barbaro applied were not obvious, the perspective had been correctly determined. Monteleone (2019, 76) shares a similar opinion in his analysis of the drawing presented by Barbaro.
63. Barbaro (1568, p. 56): “dal corpo piramidale nasce il corpo formato di quattro soperficie di sei lati, e di quattro trianguli di lati eguali.”
64. Barbaro (1568, p. 61): “due quadrati con gli anguli loro egualmente distanti, bcde, fghi, questi formano la detta soperficie di otto lati.”
65. Barbaro (1568, p. 62): “Ma se il detto corpo si posera nel piano con la figura triangulare, sia sopra’l centro a, fatto uno circulo di tanta circonferenza, che descritte in quello due sopreficie di sei lati ineguali bcdlkp, e ghimef, egualmente distanti una dall’ altra.”
66. This citation is the translation by Williams and Monteleone (2021, p. 214) of the words that Barbaro (1568, p. 63) wrote: “e si acconciera l’errore dello intagliatore nella figura 12 con le regole dette.”
67. According to Wood (2003, pp. 243), six single-leaf woodcut prints appeared in a print market in Munich in 1997 that were “completely unknown to the scholarly literature”. Figure 31 is similar to one of the six woodcuts, specifically the one Wood (2003, p. 245) shows as Fig. 13, entitled “Geometric Solids and Figures among Architectural Ruins”.
68. Andrews (2022, p. 196) says that “Stöer (…) was an active participant in a learned community of artisans who were all following each others’ experiments with geometry, owned each other’s books, and executed copies of geometries they found interesting or visually appealing”.
69. Wood (2003, p. 242) notes that “various drawings in the album bear the dates 1562, 1564, 1584, and 1599. They seem to have been bound together about 1600.
70. According to Gluch (2008, p. 842), who adds that the “drawings of geometric solids in seemingly endless variety, (…) can largely be grouped into four series. The first and second series mainly present the Platonic solids in different positions and combinations, with closed and diaphanous surfaces. In comparison, the third group shows advanced designs and an increased playfulness. Here Stöer depicts triangles, wreaths, pyramids, and cones in a multitude of variations.” On the other hand, Andrews (2022, p. 193) suggests that “the drawings were compiled by someone with an awareness of the underlying structure ordering Stöer’s geometrical investigations, but without the patience to make sure the bound volume consistently reflected it.”
71. Stöer (1600) drew the following Archimedean Solids (some in clearly non-uniform versions) in the following pages of Geometria et Perspectiva Corporata et Regulata: cuboctahedron (title page, and pp. 18, 32, 39, 87, 140, 150, 156, 187, 188, 238, 242, 250, 258, 288, 290, 308, 312, 332), icosidodecahedron (title page, and pp. 118, 133, 183, 184, 185, 190, 191, 293, 332, 333), truncated tetrahedron (pp. 53, 55, 56, 62, 102), truncated cube (pp. 17, 33, 38, 149, 230, 234, 248, 266, 289, 291, 324, 334), truncated octahedron (pp. 79, 81, 83, 86, 87, 175, 198, 201, 248, 259, 276, 300, 314, 334), truncated dodecahedron (p. 119), truncated icosahedron (pp. 134, 318), rhombicuboctahedron (title page, and pp. 24, 34, 39, 151, 188, 253, 287, 295, 299, 312, 332), rhombicosidodecahedron (pp. 171, 178, 197, 200), rhombitruncated cuboctahedron (p. 10), and the rhombitruncated icosidodecahedron (pp. 120 and 167).
72. Bombelli/Bortolotti (1929, p. 293): “Delli soprascritti cinque corpi ne nascano infiniti de lati eguali, et d’ angoli solidi pari, ma non di superfici simile, perché come si e detto quelli che hanno le superfici simili non possono essere se non cinque; de quali cinque, tagliando li lor angoli in due modi, ne nasceranno altri corpi de lati eguali, et la maggior parte di superfici dissimili.”
73. We are grateful to Dirk Huylebrouck for sharing information about the books Simon Stevin wrote.
74. Stevin (1583, p. 46): “Liber Tertivs de qvinqve regvlarium, qvinque auctorum Regularium & nouem Truncatorum regularium corporum eidem sphaerae inscriptibilium descriptione.”
75. According to the WordSense Online Dictionary (2023).
76. Pacioli (1509) describes the “Tetraedrum elevatum”, “Hexaedrum elevatum”, “Octaedrum elevatum”, “Icosaedrum elevatum”, and “Dodecaedrum elevatum” in Chapters XLVIII, XLIX, L, LI, LII of Pars Prima; Leonardo illustrates them in Plates V, VI, XI, XII, XIX, XX, XXV, XXVI, XXXI, XXXII. Stevin (1583, p. 49) names the same solid bodies as “tetraedrum auctum”, “Hexaedrum auctum”, “octoedrum auctum”, “dodecaedrum auctum”, and “icosaedrum auctum”.
77. Camerarius (1532, p. 150) translates the words of Dürer into: “In his etiam corporibus super singulas superficies planas poteris statuere punctum acutum, altum, aut depressum facere, tot quidem angulorum quot fuerint anguli in siperficie super quam steterit punctus.”. We translated these into: In these bodies, too, you will be able to turn each flat surface into a sharp point, adding height or introducing a depression, with as many angles as there are angles in the surface on which the point rests.
78. According to Crone, Dijksterhuis, Forbes, Minnaert and Pannekoek (1955, pp. 124–125), “All Stevin had to go by was Euclid’s Elements, Book XIII, the so-called XlVth, XVth, and XVIth books, which Clavius also had translated, and Dürer’s Underweysung der Rechnung mit dem Zirckel und Richtscheyt of 1525”.
79. Stevin (1583, p. 46): “…sed cum talium corporum originem vel nomina apud neminem inveniremus tamen existimaremus non sine aliquo certo fundamento consistere, vidimus tandem regularia corpora ipsorum esse scatebram, nam illorum vnum, erat tetraedrum truncatum, altera tria, truncate cubi, et quintum, truncatum octoedrum: Sexti vero corporis truncatio haec scribentibus nobis erat ignota, quamvis ex truncato cubo originem habere non dubitamus.”
80. Stevin names the first nine bodies in Fig. 34 as: “truncatum tetraedrum per laterum tertias” (truncated tetrahedron), “truncatus cubus per laterum divisiones in tres partes” (truncated cube), “bitruncatus cubus primus” (rhombicuboctahedron), “bitruncatus cubus secundus” (rhombitruncated cuboctahedron), “Truncatus cubus per laterum media”, also named “truncatum octoedrum per laterum media” (cuboctahedron), “octoedrum truncatum per laterum tertias” (truncated octahedron), “truncatum dodecaedrum per laterum divisiones in tres partes” (truncated dodecahedron), “truncatum dodecaedrum per laterum media” also named “truncatum icosaedrum per laterum media” (icosidodecahedron), and [truncatum] “icosaedrum per laterum tertias” (truncated icosahedron).
81. Stevin (1583, p. 47): “Si forte ab alio ante nos sunt inventa (de quo ferè non dubitarem propter magnam diligentiam veterum in formarum inquisitione) fatemur hoc nos ignorare. Quare vt pro nostro invento talia edimus.”
82. Stevin (1583, p. 53) says that This body is similar to the icosahedron truncated in the edges’ midpoints treated in the subsequent Definitio 21 which we translated from: “Hoc corpus simile est truncato icosaedro per laterum media sequentis 21 definitionis”. In the other note, Stevin (1583, p. 54) says that This body is similar to the dodecahedron truncated in the edges’ midpoints in the precedent Definitio 19, translated from: “Hoc corpus simile est truncato dodecaedro per laterum media precedentis 19 definitionis.”
83. Stevin (1583, pp. 82–83): “Planorum vero dispositio corporis truncati (cuius est facta mentio in principio huius 3. lib.) cuius truncandi modus haec scribentem me latebat talis est: Disponantur, vt infra, sex quadrata & 36 trianguli. Sed propter ipsius truncationis, seu verae originis ignorantiam non potuimus hoc Geometrice antedictae sphaerae inscriptibile cum ceteris construere.”
84. The following synthesizes the most common procedures to model the Archimedean Solids, which are detailed in Wenninger (1975, pp. 20–32), Pugh (1976, pp. 15–20), Gheorghiu and Dragomir (1978, 207–220), and Ostermann and Wanner (2014, pp. 282–287)
    • Cuboctahedron: truncating the vertices of the cube or octahedron in the edges’ midpoints;
    • Icosidodecahedron: truncating the vertices of the dodecahedron or icosahedron in the edges’ midpoints;
    • Truncated Tetrahedron: dividing the edges of the tetrahedron into three equal parts and truncating its vertices;
    • Truncated Octahedron: dividing the edges of the octahedron into three equal parts and truncating its vertices;
    • Truncated Icosahedron: dividing the edges of the icosahedron into three equal parts and truncating its vertices;
    • Truncated Cube: dividing the edges of the cube into three unequal parts and truncating its vertices;
    • Truncated Dodecahedron: dividing the edges of the dodecahedron into three unequal parts and truncating its vertices;
    • Rhombicuboctahedron: dividing the edges of the cuboctahedron into two equal parts, truncating its vertices, and modifying the rectangular faces into squares;
    • Rhombicosidodecahedron: dividing the edges of the icosidodecahedron into two equal parts, truncating its vertices, and modifying the rectangular faces into squares;
    • Rhombitruncated cuboctahedron: dividing the edges of the cuboctahedron into three equal parts, truncating its vertices, and modifying the irregular faces into regular;
    • Rhombitruncated icosidodecahedron: dividing the edges of the icosidodecahedron into three equal parts, truncating its vertices, and modifying the irregular faces into regular;
    • Snub cube: rotating the faces of the cube (clockwise/counterclockwise) and expanding them (or vice-versa) until regular triangular faces fill the space between them;
    • Snub dodecahedron: rotating the faces of the dodecahedron (clockwise/counterclockwise) and expanding them (or vice-versa) until regular triangular faces fill the space between them.
85. Examples of the former are: Rafael Bombelli, who described three Archimedean Solids; Heinrich Vogtherr the younger (1490–1556) whose collection of portraits c. 1545 depicts a truncated cube and a cuboctahedron, as noted by Williams (2021, p. 29); and Heinrich Lautensack, whose Des Circkels unnd Richtscheyts, auch der Perspectiva (1564) only includes a cuboctahedron. Examples of the latter are: Hieronymus Rodler (1531), Wolfgang Schmid (1539), Erhard Schön (1538–1542), Nicolo Tartaglia (1560a; b) and Jehan Cousin (1560). Andersen (2009, pp. 739–746), Friedman (2019, pp. 67-77) and Wade (2012, p. 274) mention other authors still who published several studies on perspective and solid geometry, such as Jean de Aefe, Henry Billingsley, John Dee, Jean Dubreill, Francesco Maurolico, Erhard Ratdolt, Peter Ramus, and Michael Stifel. They have not been included in this study, either because they published their works after 1600 or because we were not able to access them.
86. According to Andrews (2016a, p. 420), “In the first book of his “De Varia commensuración para I.a escultura y arquitectura (1585), Juan de Arfe (1535–1603) copies Hirschvogel’s polyhedral drawings but chooses to temper the overabundance of construction lines by stripping away half of them to reveal the net on its own.”
87. In the table of contents, Kepler (1619) names Book II as the Architectonic: “Secundus Architectonicvs, seu ex Geometria Figvrata, De Figurarum Regularium Congruentia in plano vel solido.”
88. Field (1997, p. 269): “We are free to imagine that he [Dürer] in fact knew all the Archimedeans, for judicious replacement of squares by pentagons in the nets he provides will give us all thirteen uniform polyhedra. Kepler, who certainly knew Dürer’s work, may have recognized this – which would help to explain why he claims no originality for his own work on the Archimedeans.”
89. Field (1997, p. 273) notes that “Kepler seems to have had little esteem for most of his own and immediately preceding generations”, especially those he criticized for “their lack of sustained mathematical argument, and their neglect of precise definitions,” and adds that Kepler might have underestimated, or even disregarded the studies by Piero, Pacioli, Leonardo and Barbaro.
90. The following authors discuss the possibility that Pacioli, Leonardo, Dürer, and other authors used material models of polyhedra: Malkevitch (2013, p. 57), Kemp (1992, p. 62), Field (1997, p. 262), Peiffer (2000, p. 87), Friedman (2019, pp. 37–38, 84), Scolari (2015, p. 219), and Andrews (2022, pp. 47–48). Field (1997, p. 268) notes that “Kepler, who was a very good mathematician indeed, made actual models of geometrical solids he was investigating.”
91. The identity of this person as Guidobaldo da Montefeltro, the Duke of Urbino, according to Baldasso (2010, pp. 97–98), seems to be the most plausible.
92. Coxeter et al. (1954, p. 402) note that Pacioli added the icosihexahedron, which we know as rhombicuboctahedron, to his translation of Piero’s Libellus into Italian.
93. This paragraph joins Sections 55b and 55c of Plato (1925), translated by Lamb.
94. Friedman (2019, pp. 83–85) identifies the act of Pacioli folding a rectangular piece of paper to explain “how to make immediately a material set square accurately without a compass” as “the first clearly expressed reference to folding, which conceptualizes it in a geometrical context.”
95. Max Steck (1948, Tafel XVIII): “Abb. 67. Pacioli. Dodekaeder-Netz aus “Divina Proportione” Venedig 1509. Zeichnung von Leonardo da Vinci”.
96. Andrews (2016b, p. 37) notes that Steck did not provide evidence of the location of this drawing, adding that “If it exists at all, the drawing was more likely drawn or inserted into the margins of a copy of Divina Proportione sometime after the publishing of the Underweysung”.
97. We are grateful to Cornelie Leopold, Dénes Nagy and Marta Oliveira for their contribution to the translation of the words of Dürer (1525, before drawing 29): “Wie ich das hernach aufgethan / zugettan in grund gelegt / und darnach aufgezogen alles hab aufgerissen.”
98. We chose to translate “zwifach gepabt papier” into double-thick paper, assuming it might be a paper reinforced by gluing two sheets of paper. According to Dürer’s instructions, only one of the sides of the reinforced paper is to be cut with a sharp knife to allow adjacent faces to be bent.
99. We are immensely grateful to Marta Oliveira for her precious help on the difficult translation of the words of Dürer (1525, after drawing 34): “Auch sind noch vill hübscher corpora zümachen / die auch in einer holen kugel mit all jren ecken an rüren / aber sie haben vngleyche felder / der selben wil jch eins teyls hernach auf reyssen / vnd gantz aufgethan / auf das sie ein netlicher selbs zamen müg legen / welicher sie aber machen will der reyß sie grösser auf ein zwifach gepabt papier / vñ schneyd mit einem scharpfen messer auf der einen seyten all ryß durch den einen pogen papiers / vnd so dan all ding auß dem vbrigeñ papier geledigt wirt / als dan legt man das corpus züsamen / so lest es sich geren in den rissen piegen / darumb nym des nachfolgeten auf reyssens acht / dan soliche ding sind zü vill sachen nüz.”
100. If the square faces have edge length 10, for the sphere to contain the apexes of the pyramids, the triangular faces, would have to be isosceles, with two edges equal to 9.8005.
101. Dürer (2000, 129–130) vividly mentions their friendship in the first pages of his treatise. Kemp (1992, p. 55) refers to Pirckheimer as Dürer’s closest confident.
102. In the first edition of his treatise, Dürer mistakenly identifies this drawing as number 34 instead of 43. He renumbered it by hand in the copy he was reviewing for a second edition, as shown in Fig. 38. Hieronymus Andreae would correct this detail in the posthumous edition.
103. We are very grateful to Marta Oliveira for her help in translating Dürer (1525, after drawing 42): “So du sechs recht fierung an einander sezt / und zwelf Driangel da ein netlicher so hoch ist als ein seyten der fierung und dann diß alles züsamen legest / wirt ein corpus / darauß solichs ist hernach offen aufgerisssen.”
104. According to Polthier (2003), unfolding is the process of cutting a polyhedral surface along certain curves and flattening the surface onto the plane without overlapping, while edge unfolding only allows cuts along edges, and not through the interiors of faces.
105. Williams (2021, p. 32) translates Barbaro’s words in the manuscript Ms. It. IV, 39 = 5446, fol. 30r “perspettive estender di qualunque corpo la supeficie sua in piano… che la si possa poi da quella dilatazione redur in forma corporale: accioche poi con il corpo materiale in mano apertamente di che ordine sia esso corpo veder si possa, et intender la sue altitudine per poter poi metter il perfetto suo nel quandrato, e da quello nel piano” into “Perspective is extending the surfaces of any [regular] body onto planes… so that it can then be reduced from that dilatation into corporal form. Then, with the material body in hand it is possible to plainly see of what order this body is and understand its heights, to then be able to place its perfect in the square, and from that into the plane.”
106. Barbaro (1568, p. 45): “Nel descrivere i corpi si serverà quest’ordine, che nel primo luoco poneremo le loro spiegature, dapoi le loro piante perfette, e digradate, e finalmente i dritti, e le loro adombrationi. Spiegature io intendo le descrittioni delle figure aperte, dellequali si fanno i corpi sodi piegandole infieme per dimostratione del vero, cosa veramente commoda per la pratica, e dilettevole per formare molti corpi in lanterne, e altri usi di piacere.”
107. According to Ostermann e Wanner (2014, p. 286), to obtain the vertices of the snub cube inside a cube, the faces of the cube must be scaled in the factor 0,43759 and rotated in the angle 16^o28′ (16,46667^o) clockwise or counter-clockwise (respectively yielding the laevo or dextro versions of the snub cube). With this procedure, the shortest distance between each vertex of the snub cube and the closest edge of the surrounding cube is 0.352201128739 and 0.228155493654. In the model we built with algorithmic modelling software, the edge length of the cube is 10.0, while the edge length of the snub cube is 0.437593286001.
108. Coxeter (1973, p. 11) notes that “alternate vertices of any even-faced simply-connected map can be picked out in a consistent manner” as, for instance, picking alternate vertices of a cube defines two tetrahedra. Coxeter (1973, p. 154) explains that this partial truncation can be done to any simply connected polytope or honeycomb by alternating their vertices, as long as every face has an even number of sides.
109. La Pratica della Perspettiva includes solid bodies devised from other procedures. Viana (2023a, 318–319) discusses a possible procedure to convert triangular faces into hexagonal ones in a solid body that Barbaro briefly describes in Chapter XXXIV.
110. For an octahedron with an edge length of 10.0, the edge length of the hexagons thus obtained is 2.0 while, in the uniform rhombitruncated cuboctahedron, it is 1.9526.
111. In the opinion of Schreiber et al. (2008, p. 463), this woodblock, which the authors identify as number 14, illustrates the net of the octahedron with marks showing how to get the net of the rhombitruncated cuboctahedron and the truncated octahedron from it.
112. Although very different from our interpretation, Stöer (1600, folios 266, 269 and 287) drew examples of solid bodies with concavities derived from extrusions.
113. Rotgé (1984, 22) explains that the vertices of the snub cube and the snub dodecahedron are respectively obtained by dividing the edges of the octahedron and icosahedron in the ratios 1.839286755 and 1.943151259.
114. For an octahedron with an edge length of 10.0, the triangular faces coplanar to the octahedron have an edge length of 3.214. In contrast, the square faces have 3.431, and the edge connecting each pair of triangular faces has an edge length of 3.316 (the first edge length is 3.2145502537; the second and third, 3.4318767137 and 3.3166247903).
115. Andrews (2022, p. 67) notes that Nuremberg was at the heart of German humanism and its level of wealth rivalled that of Florence: “Flush with celebrated thinkers artists, astronomers, instrument makers, printers, and a rapaciously wealthy and entrepreneurial merchant class, Nuremberg’s prosperity and prestige made it an exceptional proving ground for the synthesis of science and art.”
116. Wade (2012, p. 208) notes that only 36 watercolours are known from this author whose work, similar to the later work by Stöer, “seem to have been more private productions (…) more likely (…) simply drawn for personal satisfaction.”
117. For instance, Andersen (2009, pp. 152–155) and Monteleone (2019, pp. 69–71).
118. We express our gratitude to Kim Williams and Cosimo Monteleone for the discussion on the Italian and German connections in the sixteenth century.
119. We express our immense gratitude to Marta Oliveira for her help in translating the words of Hirschvogel (1543, Beschluß des zweiten Teils): “Wiewol ich noch vil schöner Corpora darzugehörig / hab / seind aber nicht alle gefertigt / So aber Gott will / so sollen solche in kürz auch in Druck kummen / mitsampt anderen schönen verborgen stücken”.

References

• Andersen, Kirsti. 2009. The geometry of an art: The history of the mathematical theory of perspective from Alberti to Monge. Berlin: Springer. Google Scholar 
• Andrews, Noam. 2016a. Albrecht Dürer’s personal Underweysung der Messung. Word and Image 32 (4): 409–429. https://doi.org/10.1080/02666286.2016.1216821.
• Andrews, Noam. 2016b. Irregular Bodies: Polyhedral Geometry and Material Culture in Early Modern Germany. Doctoral dissertation, Harvard University, Graduate School of Arts and Sciences
• Andrews, Noam. 2022. The polyhedrists: Art and geometry in the long sixteenth century. Cambridge: The MIT Press. Google Scholar 
• Androuet du Cerceau, Jacques II. 1576. Leçons de perspective positive, fl. 1549–1584. https://archive.org/details/leconsdeperspect00andr
• Armstrong, Walter, and Graves, Robert. 1886. Bryan’s Dictionary of painters and engravers, Biographical and Critical. George Bell and Sons. https://archive.org/details/cu31924092716970/page/n6/mode/1up?view=theater
• Axworthy, Angela. 2021. François de Foix-Candale. Motion and Genetic Definitions in the Sixteenth-Century Euclidean Tradition. Frontiers in the History of Science. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-95817-6_4
• Baldasso, Renzo. 2010. Portrait of Luca Pacioli and disciple: A new mathematical look. The Art Bulletin 92 (1–2): 83–102. https://doi.org/10.1080/00043079.2010.10786141.Article  Google Scholar 
• Ball, Walter, and Coxeter, Harold 1987. Mathematical recreations and essays. New York: Dover Publications.
• Banker, James. 2005. A Manuscript of the Works of Archimedes in the Hand of Piero della Francesca. The Burlington Magazine, March 2005, Vol. 147, No. 1224, Drawings, Prints, Manuscripts, Letters (March 2005), Burlington Magazine Publications Ltd. 165-169.
• Barbaro, Daniele. 1568. La pratica della perspettiva: opera molto vtile a pittori, a scvltori, e ad architetti: con due tauole, una de’ capitoli principali, l’altra delle cose piu notabili contenute nella presente opera. Venice: Camillo e Rutilio Borgominieri. https://www.e-rara.ch/zut/content/titleinfo/1619603
• Barbaro, Daniele, and Williams, Kim and Monteleone, Cosimo (Translators). 2021. Part III, which treats the ways of raising the body from the plan. Daniele Barbaro’s Perspective of 1568. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-76687-0_6
• Barbaro, Daniele. n.d. [La pratica della perspettiva, manuscript in Italian]. Ms. It IV, 39=5446. Biblioteca Nazionale Marciana, Venice.
• Bombelli, Rafael and Bortolotti, Ettore (Editor). 1929. L’ Algebra, Opera di Rafael Bombelli da Bologna Libri IV e V Comprendenti “La Parte Geometrica” Inedita Tratta dal ms. B 1569 (della) biblioteca dell’Archiginnasio di Bologna. Zanichelli. https://storage.lib.uchicago.edu/pres/2005/pres2005-188.pdf
• Bovelles, Charles de. 1510. Que hoc volumine continentur. Liber de intellectu. Liber de sensu. Liber de nichilo. Ars oppositorum. Liber de generatione. Liber de sapiente. Liber de duodecim numeris. Epistole complures. Insuper mathematicum opus quadripartitum. De numeris perfectis. De mathematicis rosis. De geometricis corporibus. De geometricis supplementis, NuBIS, bibliothèque numérique de la Bibliothèque interuniversitaire de la Sorbonne. https://nubis.bis-sorbonne.fr/ark:/15733/mv5t
• Centofanti. Mario. 2016. Egnazio Danti (1536–1586). Cigola, M. (eds) Distinguished Figures in Descriptive Geometry and Its Applications for Mechanism Science. History of Mechanism and Machine Science, vol 30. Springer, Cham.https://doi.org/10.1007/978-3-319-20197-9_6
• Ciocci, Argante. 2017. Luca Pacioli: La Vita e le opere. University Book.
• Ciocci, Argante. 2021. Federico Commandino and the Latin edition of pappus’ collection. Archive for History of Exact Sciences.https://doi.org/10.1007/s00407-021-00284-1
• Cousin, Jehan 1560. Libres de Perspetive. https://archive.org/details/gri_33125008282861/page/n137/mode/2up
• Coxeter, Harold. 1973. Regular Polytopes. New York: Dover Publications. Google Scholar 
• Coxeter, Harold, Michael Longuet-Higgins, and Jeffrey Miller. 1954. Uniform Polyhedra. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 246 (916): 401–450. https://doi.org/10.1098/rsta.1954.0003.Article  MathSciNet  Google Scholar 
• Cromwell, Peter. 1997. Polyhedra. Cambridge: Cambridge University Press. Google Scholar 
• Cundy, Martyn, and A. P. Rollett. 1989. Mathematical models. Norfolk: Tarquin Pub.
• Dürer, Albrecht. 1525. Underweysung der messung mit dem zirckel unD richtscheyt, in Linien ebnen unnd gantzen corporen. https://www.digitale-sammlungen.de/en/details/bsb00095496
• Dürer, Albrecht. 1538. Underweysuug der Messung, mit dem Zirckel vnd richtscheyt, in Linien Ebnen vñ gantzen Corporen. http://dl.ub.uni-freiburg.de/diglit/duerer1538/0158/thumbs?sid=64dd6e6a589d4a15120005c8f555bfde
• Dürer, Albrecht and Camerarius, Joachim (Translator) 1532. Alberti Dvreri Institvtionvm Geometricarvm Libri Qvatvor: Nunc iterató editi, servato ordine & figuris, sicut ab ipso authore expressae suerunt. https://www.digitale-sammlungen.de/en/details/bsb10863150
• Dürer, Albrecht, and Jeanne Peiffer (Translator). 2000. De la medida. Madrid: Ediciones Akal.
• Field, Judith. 1997. Rediscovering the Archimedean Polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler. Archive for History of Exact Sciences 50: 241–289. https://doi.org/10.1007/BF00374595.Article  MathSciNet  Google Scholar 
• Foix-Candale, François de. 1578. Euclides: Elementa. https://www.deutsche-digitale-bibliothek.de/item/GGYS47L7D4OY6PORJXZB7PSHKEYY2ELZ
• Francesca, Piero della. circa 1460. Trattato d’Abaco. https://commons.m.wikimedia.org/wiki/Trattato_d’abaco_by_Piero_della_Francesca
• Francesca, Piero della. circa 1480. Libellus De Quinque Corporibus Regularibus. https://commons.wikimedia.org/wiki/Libellus_De_Quinque_Corporibus_Regularibus_de_Piero_della_Francesca
• Friedman, Michael. 2019. History of Folding in Mathematics: Mathematizing the margins. Birkhauser.
• Friedman, Michael, and Lisa Rougetet. 2017. Folding in recreational mathematics during the 17th–18th centuries: Between geometry and entertainment. Acta Baltica Historiae et Philosophiae Scientiarum 5 (2): 5–34. https://doi.org/10.11590/abhps.2017.2.01.
• Gessner, Samuel, Ulf Hashagen, Jeanne Pfeiffer, and Dominique Tournès. 2018. Mathematical instruments between material artifacts and ideal machines: Their scientific and social role before 1950. Oberwolfach Reports 14 (4): 3471–3560. https://doi.org/10.4171/owr/2017/58.Article  MathSciNet  Google Scholar 
• Gheorghiu, Adrian, and Virgil Dragomir. 1978. Geometry of structural forms. London: Applied Science Pub. Google Scholar 
• Giocondi, Michele. 2021. Sottile – Dizionario dei Sinonimi e Dei contrari – corriere.it. Corriere della Sera. (n.d.). https://dizionari.corriere.it/dizionario_sinonimi_contrari/S/sottile.shtml
• Gluch, Sibylle. 2008. Geometria et perspectiva: Corpora regulata et irregulata by Lorenz Stöer. The Sixteenth Century Journal, Vol. 39, No. 3 (Fall, 2008), 842-843. https://www.jstor.org/stable/20479063
• Grünbaum, Branko. 2009. An enduring error. Elemente Der Mathematik 64: 89–101.Article  MathSciNet  Google Scholar 
• Halt, Peter. 1625. Perspectivische Reiss Kunst. Getruckht durch David Franckhen in Verlag des Authoren. https://archive.org/details/perspectiuischer00halt/page/n234/mode/thumb
• Halt, Peter. 1626. Drey Wichtige newe Kunststück in underschidlichen Perspectivischen Instrumenten inventiert und erfunden https://www.digitale-sammlungen.de/en/view/bsb00021627?page=,1
• Hart, George. 1998. Fra Giovanni’s Intarsia Polyhedra. http://www.georgehart.com/virtual-polyhedra/intarsia.html
• Hirschvogel, Augustin. 1543. Ein aigentliche vnd grundtliche anweysung in die Geometria, sonderlich aber, wie alle Regulierte vnd Vnregulierte Corpora in den grundt gelegt, vnd in das Perspecktiff gebracht, auch mit jren Linien auffzogen sollen warden. https://www.digitale-sammlungen.de/en/view/bsb00024646?page=,1
• Huylebrouck, Dirk. 2015. Lost in edition: Did leonardo da vinci slip up? Leonardo 48 (5): 458–464.Article  Google Scholar 
• Huylebrouck, Dirk, and Angelo Mingarelli. 2020. Leonardo’s folio 735 of the Codex Atlanticus How Leonardo discovered more solids than those mentioned in ‘De Divina Proportione’. Incontri. Rivista Europea di Studi Italiani 35 (1): 59–67. https://doi.org/10.18352/incontri.10334.
• Ippolito, Alfonso and Bartolomei, Cristiana (2016). Niccolò Tartaglia (1500c.–1557). In: Cigola, M. (eds) Distinguished Figures in Descriptive Geometry and Its Applications for Mechanism Science. History of Mechanism and Machine Science, vol 30. Springer, Cham. https://doi.org/10.1007/978-3-319-20197-9_4
• Jamnitzer, Wentzel. 1568. Perspectiva Corporum Regularium. https://archive.org/details/gri_33125012889602
• Jamnitzer, Wentzer, and Flocon, Albert (Pref.) and Amo, Helena del (Translator). 2006. Perspectiva Corporum Regularium. Ed. Siruela.
• Johnson, Norman. 1966. Convex Polyhedra with Regular Faces. Canadian Journal of Mathematics 18: 169–200. https://doi.org/10.4153/cjm-1966-021-8.Article  MathSciNet  Google Scholar 
• Jones, Alexander. 1986. Pappus of Alexandria, Book 7 of the Collection. Springer, New York. https://doi.org/10.1007/978-1-4612-4908-5
• Kemp, Martin. 1992. The science of art: Optical themes in western art from Brunelleschi to Seurat. New Haven: Yale University Press. Google Scholar 
• Kepler, Johannes. 1619. Harmonices Mundi. https://ia800308.us.archive.org/33/items/ioanniskepplerih00kepl/ioanniskepplerih00kepl.pdf
• Lautensack, Heinrich. 1564. Der Circles und Richtscheyts. https://digi.ub.uni-heidelberg.de/diglit/lautensack1564/0001
• Lechêne, R. 2020. The Gutenberg press. Encyclopædia Britannica. https://www.britannica.com/topic/printing-publishing/The-Gutenberg-press
• Lencker, Johannes. 1567. Perspectiva Literaria. http://www.mathe.tu-freiberg.de/7Ehebisch/cafe/lencker/perslit2.html/
• Malkevitch, Joseph. 2013. Milestones in the History of Polyhedra. In Senechal, Marjorie. 2013. Shaping space: Exploring polyhedra in nature, art, and the geometrical imagination. Springer, 53-64.
• Monteleone, Cosimo. 2019. The perspective of Daniele Barbaro. Nexus Network Journal 22 (1): 61–90. https://doi.org/10.1007/s00004-019-00468-x.Article  Google Scholar 
• Grieb, Manfred (Editor). 2007. Nürnberger Künstlerlexikon: Bildende Künstler, Kunsthandwerker, gelehrte, Sammler, kulturschaffende und mäzene vom 12. Bis zur Mitte des 20. jahrhunderts. Munich: De Gruyter Saur
• Ostermann, Alexander, and Gerhard Wanner. 2014. Geometry by Its History. Berlin: Springer. Google Scholar 
• Pacioli, Luca. 1494. Summa de Arithmetica, Geometria, Proportione et Proportionalita. Retrieved from https://www.e-rara.ch/zut/content/titleinfo/2683230
• Pacioli, Luca, and Resta, Ricardo (Translator). 2013. La divina proporcion. Buenos Aires: Losada.
• Pacioli, Luca and Vinci, Leonardo da. 1509. Divina Proportione. https://archive.org/details/divinaproportion00paci/mode/2up
• Peiffer, Jeanne. 2002. La géométrie d’Albrecht Dürer et ses lecteurs. Bulletin de l’Association des Professeurs de Mathématiques de l’Enseignement Public, 442, 630-648. https://www.apmep.fr/IMG/pdf/AAA02054.pdf
• Peiffer, Jeanne. 2004. ‘Projections Embodied in Technical Drawings: Dürer and His Followers,’ Lefèvre, Wolfgang (Editor) Picturing Machines, Cambridge, MA: MIT Press, 245–275
• Peters, Jane. 2003. “Hirschvogel.” In Grove Art Online. http://www.oxfordartonline.com.proxy.lib.fsu.edu/subscriber/article/grove/art/T038266pg2
• Pfaff, Dorothea. 1996. Lorentz Stöer: “Geometria et Perspectiva.’’. Master of Arts: Faculty of History and the Arts, Ludwig-Maximilians-Universität München. Google Scholar 
• Pfinzing, Paul. 1599. Ein schöner kurtzer Extract der Geometriae vnnd Perspectiuae : wie die Perspectiua ohne Geometria nicht sein kan, Hernacher wie die Perspectiua in ihren Wercken auff drey Weg zuuerstehen. http://digital.bib-bvb.de/view/bvb_mets/viewer.0.6.5.jsp?folder_id=0&dvs=1693476769032~220 &pid=162690 &locale=en &usePid1=true &usePid2=true
• Pfinzing, Paul. 1616. Optica, das ist Gründtliche doch Kurtze Anzeigung Wie nothwendig die Löbliche Kunst der Geometriae seye inn der Perspectiv https://dlc.mpg.de/image/868445738/5/LOG_0000/
• Plato and Lamb, Walter (Translator). 1925. Timaeus. Cambridge: Harvard University Press; London, William Heinemann Ltd., Perseus Digital Library.
• Polthier, Konrad. 2003. Imaging maths – Unfolding polyhedra. https://plus.maths.org/content/imaging-maths-unfolding-polyhedra
• Pugh, Anthony. 1976. Polyhedra: A visual approach. Berkeley: University of California Press.Book  Google Scholar 
• Rodler, Hieronymus. 1531. Perspectiua eyn schön nützlich Büchlin vnd Vnderweisung der Kunst des Messens mit dem Zirckel, Richtscheidt oder Linial. https://archive.org/details/bub_gb_PrgwhRCoZUYC
• Rotgé, Jean-François. 1984. Rotating polyhedra with congruent plane pentagonal faces. Structural Topology 9: 15–30.MathSciNet  Google Scholar 
• Schmid, Wolfgang. 1539. Das erst buch der Geometria. https://reader.digitale-sammlungen.de/de/fs1/object/display/bsb10164586_00007.html
• Schmitt, Annegrit. Lautensack Hanns. 1982. Neue Deutsche Biographie 13 S. 729 https://www.deutsche-biographie.de/pnd118726757.html#ndbcontent
• Schön, Erhard. 1538-42. Unterweisung der Proportion und Stellung der Possen. https://digi.ub.uni-heidelberg.de/diglit/schoen1920/0009/info,thumbs#col_thumbs
• Schreiber, Peter, Gisela Fischer, and Maria Sternath. 2008. New light on the rediscovery of the Archimedean solids during the Renaissance. Archive for History of Exact Sciences 62: 457–467. https://doi.org/10.1007/s00407-008-0024-z.Article  MathSciNet  Google Scholar 
• Scolari, Massimo. 2015. Oblique drawing. Cambridge: MIT Press. Google Scholar 
• Scriba, Christoph, and Peter Schreiber. 2015. 5000 Years of geometry. Basel: Birkhauser Verlag GmbH.Book  Google Scholar 
• Séquin, Carlo, and Raymond Shiau. 2018. Rendering Pacioli’s Rhombicuboctahedron. The Best Writing on Mathematics 2017: 106–120. https://doi.org/10.1515/9781400888559-015.Article  Google Scholar 
• Sirigatti, Lorenzo. 1596. La pratica di prospettiua del Caualiere Lorenzo Sirigatti: al Sermo. Ferdinando Medici granduca di Toscana. c.1 https://babel.hathitrust.org/cgi/pt?id=gri.ark:/13960/t7fr2c78n&seq=22
• Steck, Max. 1948. Dürers Gestaltlehre der Mathematik und der bildenden Künste. Halle (Saale): Max Niemeyer Verlag, 1948 https://digi.ub.uni-heidelberg.de/diglit/steck1948
• Stevin, Simon. 1583. Problematum Geometricorum[SPACE]https://books.google.pt/books?id=Yz9SAAAAcAAJ&pg=PA1 &hl=pt-PT &source=gbs_selected_pages &cad=2#v=onepage &q &f=false
• Stevin, S., E. Crone, E.J. Dijksterhuis, R.J. Forbes, and J., M. M. G., and Pannekoek, A. 1955. Principal works of Simon Stevin. Swets and Zeitlinger: C.V.
• Stöer, Lorenz. 1567. Geometria et Perspectiva : HierInn Etliche Zerbrochne Gebew den Schreiner[n] In eingelegter Arbait dienstlich auch vil andern Liebhabern Zu sonder[n] gefallen geordnet vnnd gestelt. http://digital.deutsches-museum.de/item/BV010656517
• Stöer, Lorenz. 1600. Geometria et Perspectiva: Corpora Regulata et Irregulata. https://epub.ub.uni-muenchen.de/12870/1/Cim._103.pdf
• Stover, Christopher. 2023. “Rule of Three.” From https://mathworld.wolfram.com/RuleofThree.html. A Wolfram Web Resource, created by Eric W. Weisstein. https://mathworld.wolfram.com
• Tartaglia, Nicolo. 1560a. General Trattato di Numeri et Misure, Part IV. https://books.google.pt/books?id=gk9ZAAAAcAAJ&pg=PP1 &redir_esc=y#v=onepage &q &f=false
• Tartaglia, Nicolo. 1560b. General Trattato di Numeri et Misure, Part V. https://www.google.pt/books/edition/General_Trattato_Di_Numeri_Et_Misure/kk9ZAAAAcAAJ?hl=pt-PT&gbpv=1 &dq=inauthor:%22Niccol%C3%B2+Tartaglia%22+quinta &printsec=frontcover
• Taylor, C.W.W. 1997. From the beginning to Plato. London: Routledge. Google Scholar 
• Thomas, Hartwig, and Kim Williams. 2000. Fra’ Giovanni’s intarsias in Verona. The Mathematical Intelligencer 22 (2): 38–40. https://doi.org/10.1007/bf03025374.Article  Google Scholar 
• Tormey, Alan, and Judith Tormey. 1982. Renaissance Intarsia: The Art of Geometry. Scientific American 247 (1): 136–145. http://www.jstor.org/stable/24966642
• Unguru, Sabetai. 1974. Pappus in the thirteenth century in the Latin West. Archive for History of Exact Sciences 13 (4): 307–324. https://doi.org/10.1007/bf00327298.Article  MathSciNet  Google Scholar 
• Viana, Vera 2023a. Materializing Daniele Barbaro’s Creativity with 3D Printing. Judy Holdener, Eve Torrence, Chamberlain Fong, and Katherine Seaton (Editors) Proceedings of Bridges 2023: Mathematics, Art, Music, Architecture, Culture. Phoenix, Arizona: Tessellations Publishing. 313-320. https://archive.bridgesmathart.org/2023/bridges2023-313.pdf
• Viana, Vera. 2023b. Non-Uniform Polyhedra Described by Daniele Barbaro. Monteleone, Cosimo and Williams, Kim (Editors). Daniele Barbaro and the University of Padova. DBSPA 2022. Trends in the History of Science. Birkhäuser, Cham. https://doi.org/10.1007/978-3-031-29483-9_6
• Vinci, Leonardo da. 1495. Codex Atlanticus, folio 735 verso. Veneranda Biblioteca Ambrosiana and Mondadori Portfolio. https://codex-atlanticus.ambrosiana.it/#/Detail?detail=735
• Vignola, Jacopo, and Danti, Egnazio. 1583. Le due regole della prospettiva pratica / di Iacomo Barozzi da Vignola; con i comentarij del R.P.M. Egnatio Danti. https://archive.org/details/hin-wel-all-00001766-001
• Villafañe, Jean. 1585. De varia commensuracion para la esculptura y architectura. https://archive.org/details/commensuracionpa00arfe
• Wade, David. 2012. Fantastic geometry: polyhedra and the artistic imagination in the Renaissance. Glastonbury: Glastonbury Squeeze Press. Google Scholar 
• Weissbach, Bernulf, and Horst Martini. 2002. On the chiral Archimedean solids. Beiträge zur Algebra und Geometrie. Contributions to Algebra and Geometry 43: 121–133. Google Scholar 
• Weiß, Karl. 1894. Hans Tscherte. Daniele Allgemeine Deutsche Biographie, herausgegeben von der Historischen Kommission bei der Bayerischen Akademie der Wissenschaften, Band 38, S. 716–718, Digitale Volltext-Ausgabe in Wikisource, https://de.wikisource.org/w/index.php?title=ADB:Tscherte,_Hans&oldid=-
• Weixlgärtner, Arpad. 1910. Ungedruckte Stiche: Materialien und Anregungen aus Grenzgebieten der Kupfer stichkunde, Jahrbuch der kunsthistorischen Sammlungen des allerhöchsten Kaiserhauses, 29, 1910/11, pp. 259–386. https://digi.ub.uni-heidelberg.de/diglit/jbksak1910_1911/0392/image,info
• Wenninger, Magnus. 1975. Polyhedron models. Cambridge: University Press. Google Scholar 
• Wikimedia Foundation. 2023. January 15. Fondaco dei Tedeschi. Wikipedia. https://it.wikipedia.org/wiki/Fondaco_dei_Tedeschi
• Williams, Kim. 2021. Daniele Barbaro and the Geometric Solids. Kim Williams and Cosimo Monteleone (Editors). Daniele Barbaro’s Perspective of 1568. Birkhäuser, Cham.https://doi.org/10.1007/978-3-030-76687-0_1.1-57
• Williams, Kim. 2002. Plagiary in the Renaissance. The Mathematical Intelligencer 24 (2): 45–57.Article  MathSciNet  Google Scholar 
• Wood, Christopher. 2003. The perspective treatise in ruins: Lorenz Stöer, Geometria et perspectiva, 1567. Lyle Massey (Editor). The Treatise on Perspective. Studies in the History of Art. Symposium Papers XXXVI. Washington: National Gallery of Art, CASVA
• Wordsense Oline Dictionary. 2023. Auctorum? (Latin): Meaning, definition. wordsense.eu. https://www.wordsense.eu/auctorum

Acknowledgements

The author would like to express her gratitude to several individuals and institutions who supported and contributed to the development of this research. The author is grateful to Kim Williams and Cosimo Monteleone for encouraging her to develop this research. The author is immensely thankful to Marta Oliveira for her valuable help with the translations from Old German, as well as to Célia Oliveira and Marco Ginoulhiac for their assistance with translations from Latin and Italian, respectively. The author would like to express her gratitude to Dr. Christoph Metzger, Curator of the Albertina Museum in Vienna, for sharing information about the publications related to the Anonymous Author’s printing woodblocks. The author would also like to thank the Albertina Museum for allowing the reproduction of their images. Additionally, the author acknowledges the Veneranda Biblioteca Ambrosiana in Milan and Mondadori Portfolio, as well as the Biblioteca Nazionale Marciana in Venice, for their permission to reproduce the images from Leonardo da Vinci and Daniele Barbaro. The author is also grateful to the anonymous reviewers for their invaluable comments and insights and extends a heartfelt thank you to José Miguel Rodrigues and Carlos Machado from CEAU for their unwavering support of her research.

Funding

Open access funding provided by FCT|FCCN (b-on).

Author information

Authors and Affiliations

1. Centre for Studies in Architecture and Urbanism (CEAU), Faculty of Architecture, University of Porto, Porto, PortugalVera Viana

Corresponding author

Correspondence to Vera Viana.

Ethics declarations

Conflict of interest

The work has been funded by national funds through FCT – Fundação para a Ciência e a Tecnologia, I.P., under the project “UIDB/00145/2020”. The author has no relevant financial or non-financial interests to disclose.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.