printer’s log

The 3D Prints shown in this page are models of the:

Rectified Truncated Octahedron
Chamfered cube
Great dodecahedron
Small Stellated dodecahedron
Icosidodecahedron

I would love to know about your experience in 3D printing or any questions you may have. Feel free to reach out in the comments below.

The 3D printer I have been using since September 2022 is a Form 3+ that belongs to CEAU at the Faculty of Architecture of the University of Porto. It is an excellent stereolithographic printer, and several prints are stunning. Still, others have failed, mainly because my polyhedral models tend to push the printer’s limits.

Printing solid models is far too easy, so I prefer to print models without faces and replace the edges with long cylinders or “pipes.” Depending on the number and length of the edges and existing intersections, some models come out perfect, while others require an internal structure to avoid breaking during printing. Here, I will show some of my 3D prints, including the ones that failed, hoping that my experience may be helpful to anyone who is beginning to explore stereolithographic printing.

I use Rhinoceros and Grasshopper to model polyhedra (from scratch, so to speak). After editing the edges and any existing internal structure with the Multipipe tool in Grasshopper, I export the .3dm as .stl and prepare it for printing in PreForm.

Rectified Truncated Octahedron

The rectified truncated octahedron was described independently in 1568 by Wentzel Jamnitzer and Daniele Barbaro [more about the subject here and here]. I built the model shown below in Rhino and Grasshopper and 3D printed it, in addition to the other models in this paper, which I presented at Bridges Halifax 2023 Conference.

Below is an interactive 3D model of the rectified truncated octahedron and a video showing how I removed the supports from its 3D print in resin. If you have a 3D printer, you may download the STL file from this webpage.

Rectified Truncated Octahedron by vera viana on Sketchfab

vera viana removing the supports of a 3D print of the rectified truncated octahedron

Chamfered cube

I began studying the chamfered cube for the paper Materializing Daniele Barbaro’s Creativity with 3D Printing, which, in its turn, is a development of the book chapter Non-Uniform Polyhedra Described by Daniele Barbaro [2]. Amazingly, Daniele Barbaro (1514-1570) was the first to describe the chamfered cube in 1568 on page 111 of [3], but he did not show any drawings; he just referred to as the body of six squares and twelve hexagons as an example. More about modelling the chamfered cube is found here.

The first models I printed of the equilateral chamfered cube included an internal structure connecting the vertices of the inner cube, printed as a solid body, to the vertices of the chamfered cube. Printing this model without flaws was impossible because of the cube’s weight and the edge thickness. The model shown is one of many failed prints, still with its internal supports. I printed other models with short prisms instead of the square faces, which also failed.

[circumdiameter 130 mm | pipe radius: 1.5 mm]

In the following, I removed the solid cube, but many pipes still broke during printing, in some cases, because of their thickness, and in others, because of the large hexagonal faces. I could have increased the radius of the pipes, but I’m not too fond of that solution because the pipes become too thick and no longer look like edges.

[left: circumdiameter 130 mm | pipe radius: 2.0 and 1.5 mm / right: circumdiameter 110 mm | pipe radius: 1.5 and 1.0 mm]

Adding more edges to the internal structure solved some issues and even allowed to reintroduce the inner cube, but the model became somewhat confusing.

[left and right: circumdiameter 110 mm | pipe radius: 2.0 and 1.75 mm]

I also printed a model of the chamfered cube as a solid body, shown below on the right, but I wouldn’t say I like it. The one on the left was, in my opinion, the best solution.

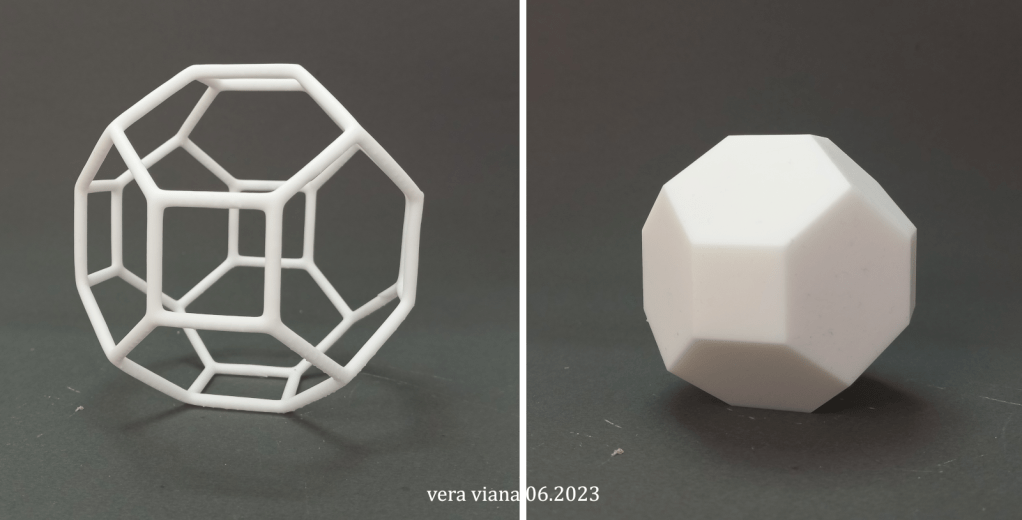
[left: circumdiameter 110 mm | pipe radius: 2.0 mm | Total printing time: 11h20; right: circumdiameter 72 mm | Total printing time: 06h40]

Great dodecahedron

Photos of the printed great dodecahedron are somewhat confusing, so I prefer to show a video of me taking out the supports (which I enjoy doing very, very much). This model took me about 20 minutes to take everything out, but the video is shown in fast-motion:

vera viana removing the supports of a 3D print of the great dodecahedron

[circumdiameter 130 mm | pipe radius: 1.5 mm | Total printing time: 12h45m]

Small stellated dodecahedron

Printing concave polyhedra can be tricky because of the self-intersecting faces. For the print to include all the edges, the model must be prepared so that the edges inside the polyhedron are distinct line segments. This way, the multipipe will work fine, but other details must be attended to depending on the edge length and model size.